一、一周知识概述

　　本周学习内容是高二（上）数学第七章第三节，即§7.3两条直线的位置关系．共用六个课时，其中第一课时通过直线的方程讨论两直线平行和垂直的充要条件，后三个课时，接着讨论从直线l1到直线l2的角及其正切公式，然后指出两条直线的交点与直线的方程的解之间的关系，并通过具体例题，说明如何求两条直线的交点，最后导出了点到直线的距离公式．最后两个课时介绍对称性问题及直线系等内容．

　　两条直线的各种位置关系是现象，抓住它们的内在联系就找到了规律，也就找到了解决问题的方法，在教学过程中让学生了解规律是现象和本质间的必然联系的辩证思想．

二、重难点知识的归纳与剖析

1、本周学习的重点是垂直与平行位置关系的确定；两条直线所成的角；点到直线的距离．

（1）两条直线l1和l2有斜截式方程时，直线l1∥l2的充要条件是：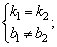

　　

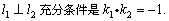
（2）两条直线的夹角

　　 l1:y=k1x＋b1，l2:y=k2x＋b2．

　　 ∴ k1·k2=－1时，l1⊥l2．

　　 当k1·k2≠－1，l1与l2夹角为θ，

　　 则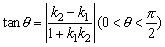

　　 l1到l2的角θ1，

　　

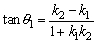
注意：

　　①角的范围．其中到角θ∈（0°，180°），夹角α∈（0°，90°]．

　　②斜率是否存在，两直线是否垂直，因为在这两种情况下公式失效，可能失根．此外在使用夹角公式可能产生增根.

（3）两条直线的交点

　　如果两条直线相交，由于交点同时在这两条直线上，交点的坐标一定是这两个方程的惟一公共解；反过来，如果这两个二元一次方程只有一个公共解，那么以这个解为坐标的点必是直线 l1和l2的交点.

　　在同一平面内两条直线有三种位置关系：相交、平行、重合 .相应的由直线方程组成的二元一次方程组的解有三种情况：有惟一解、无解、有无数多个.

　　过两条直线 l1：A1x＋B1y＋C1=0，l2：A2x＋B2y＋C2=0的交点可作无数条直线，这些直线的方程可用一个方程表示：m(A1x＋B1y＋C1)＋n(A2x＋B2y＋C2)=0（其中m、n∈R且m与n不同时为零）或用A1x＋B1y＋C1＋λ(A2x＋B2y＋C2)=0（λ∈R，但此种形式不表示直线l2）上述两种方程称为直线系方程，解题时若能恰当运用可简化运算过程.

（4）点到直线的距离

　　点P到直线l:Ax＋By＋C=0的距离为d，则：

　　

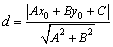
由这个公式又可得到两平行直线l1：Ax＋By＋C1=0，l2：Ax＋By＋C2=0间的距离公式：

　　．

2、本周学习的难点

　　本周学习的难点是两条直线平行与垂直及到角的讨论，处理好此类问题要有较强的数学思想、意识和全面的基础知识，对于本节中，注意以下几种数学思想方法的运用．

　　（1）数形结合思想．随着知识的积累在解题思维中，有很多题目是先画出图形，然后借助于图形找到数量关系，达到解题目的，遇到一些代数问题，也有意识地联想到图形，进而达到求解目的．

　　（2）等价转化思想．求两条直线的距离可以在其中一条直线上任取一点，再求这一点到另一直线的距离，使两条平行直线的距离转化为点到直线的距离．

　　点到直线的距离，实际上就是在直线上一动点到直线外一个定点之间最短的距离．

　　（3）分类讨论思想．研究含有字母（参数）的两直线垂直或平行时，应考虑到斜率存在或不存在两种情况．

　　研究含有字母的两直线所成的角时，应考虑到：

　　

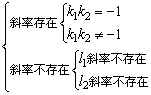
　　四种情况．

三、例题点评

例1、已知三角形一个顶点是（2，－7），由其条两个顶点引出的高线和中线所在直线方程是3x＋y＋11=0 ，x＋2y＋7=0，求此三角形三边所在直线．

[解析]

例2、光线自直线l1:2x－3y＋4=0上的点P（4，4）发出，沿直线l1经直线l:x＋5y－11=0反射，求反射光线所在的直线方程．

[解析]

例3、试求三直线ax＋y＋1=0，x＋ay＋1=0，x＋y－a=0构成三角形的条件．

[解析]

例4、经过点P（2，3）且与直线l：夹角为30°的直线方程为______________.

[解析]

例5、直线l过点A（2，3），且被两平行线l1:3x＋4y－7=0和l2:3x＋4y＋8=0截得线段长为，试求直线l的方程．

[解析]

例6、求经过两条直线2x＋3y＋1=0和x－3y＋4=0的交点，并且垂直于直线3x＋4y－7=0的直线的方程.

[解析]