|
一、一周知识概述
本周学习内容是高二(上)数学第八章的第五节、第六节,即§8.5抛物线及其标准方程,§8.6抛物线的简单几何性质,共用四个课时,具体安排如下:第一、二节课介绍抛物线的定义及其标准方程,使学生能够根据条件熟练地写出抛物线的方程,并能够利用抛物线的定义解决问题,会求抛物线的焦点弦长等.第三、四节课主要介绍抛物线的几何性质及直线与抛物线的位置关系.在此节的学习中,要使学生更进一步熟练掌握利用方程研究曲线的基本方法,培养学生对知识归纳、类比、迁移的能力.
二、重难点知识讲解
1、本周学习的重点是抛物线的定义及其标准方程,学习时,可通过与椭圆、双曲线的定义对比加深对抛物线定义的理解.
抛物线的定义可以从以下几个方面理解、掌握:
①抛物线的定义还可叙述为“平面内与一个定点F和一条直线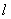 的距离的比等于1的轨迹叫做抛物线.” 的距离的比等于1的轨迹叫做抛物线.”
②定义的实质可归结为“一动三定”,一个动点,设为M;一个定点F,叫做抛物线的焦点;一条定直线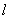 ,叫做抛物线的准线;一个定值,即点M与点F的距离和它的直线 ,叫做抛物线的准线;一个定值,即点M与点F的距离和它的直线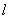 的距离之比等于1. 的距离之比等于1.
③定点F不在定直线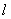 上,否则动点M的轨迹不是抛物线,而是过点F垂直于直线 上,否则动点M的轨迹不是抛物线,而是过点F垂直于直线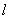 的一条直线. 的一条直线.
由于选取坐标系时设坐标轴有四种不同方法,因此抛物线有四种形式的方程.记忆这种对应关系的方法是:一次项的变量是x(或y),则x轴(或y轴)是抛物线的对称轴;一次项系数的符号决定抛物线的开口方向.
平面内到定点F和定直线l(F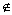 l)距离相等的点的轨迹叫抛物线,点F到直线l的距离记作p(p>0),建立适当的坐标系,使得抛物线的顶点在原点,焦点在坐标轴上,可得到如下四种形式的标准方程,其焦点坐标和准线方程如下表所示: l)距离相等的点的轨迹叫抛物线,点F到直线l的距离记作p(p>0),建立适当的坐标系,使得抛物线的顶点在原点,焦点在坐标轴上,可得到如下四种形式的标准方程,其焦点坐标和准线方程如下表所示:
抛物线方程
(p>0)
|
y2=2px |
y2=-2px |
x2=2py |
x2=-2py |
焦点坐标 |
(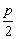 ,0) ,0) |
(-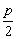 ,0) ,0) |
(0,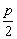 ) ) |
(0,-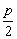 ) ) |
准线方程 |
x=-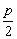 |
x=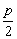 |
y=-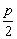 |
y=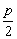 |
开口方向 |
同x轴正向 |
同x轴负向 |
同y轴正向 |
同y轴负向 |
从上表可以归纳出,对于抛物线的标准方程,焦点总在一次项的变量对应的坐标上,准线方程中的变量同标准方程中的一次项变量一致,一次项的符号决定开口方向.这些规律,便于我们讨论抛物线的性质和确定抛物线的标准方程.另应注意一次项系数为2p时,焦点、准线中为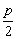 ,二者为四倍的关系. ,二者为四倍的关系.
例1、已知抛物线的顶点在原点,焦点在y轴上,且抛物线上一点(-3,m)到焦点的距离为5,求抛物线的方程.
[分析与答案]
例2、顶点在原点,焦点在x轴上的抛物线截直线2x-y+1=0所得弦长为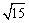 ,求此抛物线的标准方程. ,求此抛物线的标准方程.
[分析与答案]
2、本周学习的难点是抛物线的几何性质的掌握和运用.
抛物线的性质和椭圆、双曲线比较起来,差别很大.它的离心率等于1,它只有一个焦点,一个顶点,一条对称轴,一条准线,没有中心.学习时应加以注意.
抛物线的性质分范围、对称性、顶点、离心率四个方面.把握抛物线的性质,可记住这六个字“五个一”无中心.即一条准线、一个焦点、离心率为1,一个顶点,一条对称轴,为五个“一”,抛物线无中心.
例3、过点Q(4,1)作抛物线y2=8x的弦AB,恰被Q平分,求AB所在直线方程.
[分析与答案]
例4、定长为3的线段AB的两个端点在抛物线y2=x上移动,记线段AB的中点为M,求点M到y轴的最短距离,并求此时点M的坐标.
[分析与答案]
例5、设抛物线C:y2=2px(p>0),过焦点F的弦AB的倾斜角为α,|AF|=m,|BF|=n.求证:
(1)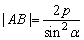 ;(2) ;(2)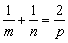 . .
[分析与答案]
3、直线与抛物线
直线与圆锥曲线的问题有交点,弦长,对称,轨迹等,处理方法基本相同,应比较前面介绍的方法解决这些问题.
例6、A、B是抛物线y2=2px(p>0)上的两点,且OA⊥OB.
求证:(1)A、B两点的横坐标之积,纵坐标之积均为定值;
(2)直线AB过定点;
(3)若OM⊥AB,求M的轨迹方程.
[分析与答案]
例7、已知抛物线的方程为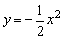 ,A、B、P三点都在抛物线上,若P(2,-2),且PA、PB的倾斜角互补. ,A、B、P三点都在抛物线上,若P(2,-2),且PA、PB的倾斜角互补.
(1)求直线AB的斜率;
(2)若直线AB在y轴上的截距大于-6,求△PAB面积的最大值.
[分析与答案]
|