|
一、一周知识概述
在本周的学习中,我们首先学习平面的基本概念,认识平面是怎样的一种图形,然后研究平面具有哪些性质,进而探索运用这些性质又可解决哪些问题,最后学习空间的平行直线与异面直线,掌握空间平行直线的传递性及应用,理解等角定理及其应用;学习异面直线的概念及其判断,掌握两条异面直线所成角的概念;进一步学习两条异面直线所成的角,会求两条异面直线所成的角.通过这一周的学习,同学们不仅可以冲破以往的在二维空间中思考问题的定式,初步构建三维模型,而且使自己对周围的事物从三维的角度有一根本性的认识.本周的学习内容是整个立体几何学的基础,为后续学习空间立体图形的性质作出铺垫,初步培养立体几何的推理能力和空间想象能力.
二、重、难点知识的归纳与剖析
(一)本周学习与研究中的两个重点
1、平面的基本概念
平面是构成空间图形的基本元素之一,是一个不加定义,只须理解的最基本的原始概念,理解它应抓住其三个特征:“平”、“无厚度”、“可以无限延展”.其中还应注意平面的画法及平面的表示方法.
平面是空间图形,也可以将它看成由一些点构成的集合,因此我们借用集合的语言来表示点、线、面间的关系.如点A在平面α内,记作A∈α;点A不在平面α内,记作A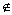 α,直线l在平面α内,记作:l α,直线l在平面α内,记作:l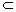 α;直线l不在平面α内,记作l α;直线l不在平面α内,记作l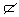 α. α.
2、平面的基本性质
平面的基本性质,教材中以三个公理及三个推论形式给出,它们分别是:
(1)公理1:如果一条直线l的两点在一个平面内,那么这条直线上所有点都在这个平面内.
图形语言表述:

符号语言表述:A∈l,B∈l,A∈α,B∈α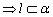 . .
(2)公理2:如果两个平面有一个公共点,那么它们还有其它的公共点,且所有这些公共点的集合是一条过这个公共点的直线.
图形语言表述:
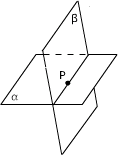
符号语言表述:P∈α∩β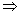 α∩β=l且P∈l. α∩β=l且P∈l.
(3)公理3:经过不在同一条直线上的三点,有且仅有一个平面.
图形语言表述:

符号语言表述:
A、B、C三点不共线 有且仅一个平面α,使A∈α,B∈α,C∈α. 有且仅一个平面α,使A∈α,B∈α,C∈α.
(4)三个推论:
① 经过一条直线和这条直线外的一点,有且仅有一个平面;
② 经过两条相交直线,有且仅有一个平面;
③ 经过两条平行直线,有且仅有一个平面.
这三个公理和三个推论,它们是研究立体几何的基本理论基础,同学们必须掌握好.一方面要理解它们的内容,分析它们的条件和结论,另一方面要体会出它们的作用:如公理1既可判定直线是否在平面内,点是否在平面内,又可用直线来检验平面;公理2既是判定两个平面是否相交的依据,又可判定点是否在直线上;公理3可用来确定平面,也可用来证明点、线共面问题.
3、空间直线的传递性及应用,等角定理及简单应用,异面直线所成的角及异面直线的概念及判定定理.
(二)本周学习与研究中的难点
1、平面的基本性质及灵活运用是本周学习与研究的第一个难点.突破这一难点的关键是我们应该加强观察了解周围事物,从对图形的直观认识上升到理性认识,反过来又用它们来检验生活实例.其中可通过回答生活中的一些实际问题来理解和记忆这些公理,如:通过回答“把文件夹的一角放在桌面上,问文件夹所在的平面与桌面所在的平面有几个公共点?”来理解公理1;通过回答“把教室门及其所在的墙看成两平面,当门不拴上时,它们的公共点分布情况如何?”来理解公理2;通过回答“把门插销插上,门便不动,为什么?”来理解公理3.
2、本周学习的第二个难点是求两条异面直线所成的角,其求法分为两步,简称“先转后算”.
(1)找角:通过平移或补形的方法将异面直线所成角转化为相交直线所成的锐角或直角.
平移:利用平行线或中位线的性质.
补形:利用正方体或其它几何体的性质.
(2)求角:将相交直线所成的锐角或直角放在一个三角形中,利用直角三角形中的三角函数或余弦定理求出这个角的大小或其三角函数值.
注意立体几何对书写格式和步骤要求较严,不能只计算必须写出推导过程.
三、例题点评
例1、下面各命题中正确的有__________.
①书桌面是平面;
②8个平面重叠起来,要比6个平面重叠起来厚;
③有一个平面的长是50m,宽是20m;
④平面是绝对的平、无厚度,可以无限延展的抽象的数学概念;
⑤平行四边形是一个平面;
⑥任何一个平面图形都是一个平面;
⑦空间图形中先画的线是实线,后画的线是虚线.
[分析、解答、点评]
例2、已知直线m与直线a,直线b分别交于A、B,且a∥b,求证:过a、b、m有且只有一个平面.
[分析、解答、点评]
例3、如图所示,在正方体ABCD—A1B1C1D1中,设线段A1C与平面ABC1D1交于Q,求证:B、Q、D1共线.
[分析、解答、点评]
例4、分别和两条异面直线相交的两条直线的位置关系是( )
A.相交 B.异面
C.平行 D.相交或异面
[分析、解答、点评]
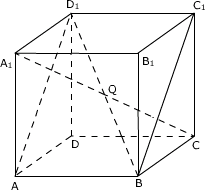
例5、如图所示,设E、F、G、H分别是空间四边形ABCD各边中点,P、Q分别是两条对角线的中点,求证:EG、FH、PQ三线共点.
[分析、解答、点评]
例6、如图所示,在空间四边形ABCD中,已知AD=1,BC=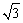 ,且AD⊥BC,对角线 ,且AD⊥BC,对角线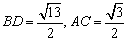 ,求AC和BD所成的角. ,求AC和BD所成的角.
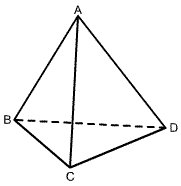
[分析、解答、点评]
|