|
一、一周知识概述
本周学习平面的基本概念和空间的平行直线与异面直线.本周的学习内容是整个立体几何学的基础.与在二维空间中思考问题的方式不同,需要构建三维模型,而且使自己对周围的事物从三维的角度有一根本性的认识.要理解和掌握平面和平面的性质,空间平行直线的传递性及应用,理解等角定理及其应用,学习异面直线的概念及其判断,掌握两条异面直线所成角的概念,会求两条异面直线所成的角.
二、重难点讲解
1、立体几何概述
立体几何主要是研究空间点、线、面和简单几何体的几何性质、位置关系、画法、计算、证明.
学习立体几何要注意以下几点:
(1)注意立体图形与平面图形的区别与联系与平面几何作适当类比.
(2)准确作图.
(3)多观察、培养自己的空间想象能力.
2、平面的基本性质
平面通常用一个希腊字母α,β,γ等来表示,如平面α、平面β、平面γ等;点A在平面α内,记A∈α,点A不在平面α内,记A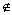 α;直线l在(不在)平面α内,记l α;直线l在(不在)平面α内,记l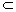 α(l α(l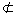 α). α).
公理1有两点作用:
(1)判定直线是否在平面内;
(2)判定一个面是否为平面.
公理2的应用为:
(1)确定交线;
(2)证明三点共线;
(3)证明三线共点.
公理3及其三个推论都可以用来证明共面问题.
例1、如图,已知△ABC三边所在的直线分别交平面α于P、Q、R,求证:P、Q、R三点在同一直线上.

[解析]
例2、已知四条直线两两相交,且不经过同一点,求证:这四条直线共面.
[解析]
3、空间两条直线的位置关系

例3、已知:四边形ABCD是空间四边形(四个顶点不共面的四边形),E、H分别是边AB、AD的中点,F、G分别是边CB、CD上的点,且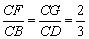 .求证:四边形EFGH是梯形. .求证:四边形EFGH是梯形.
[解析]
不同在任何一个平面的两条直线称为异面直线.
异面直线是一个重要的概念,在理解概念上,要重点抓以下三个问题:
(1)如何证明两条直线是异面直线,一般采用下面两种方法:
一是证两直线不共面,即证两直线既不相交、也不平行,注意正确运用反证法;
二是根据异面直线的判定定理:过平面外一点与平面内一点的直线,和平面内不经过该点的直线是异面直线。
证明两条直线异面常根据定义和判定定理(即课本P15例3).
例4、如图所示正方体ABCD—A1B1C1D1中,M、N分别是A1B1、B1C1的中点。问:

(1)AM和CN是否是异面直线?说明理由。
(2)D1B和CC1是否是异面直线?说明理由。
[解析]
4、异面直线所成的角
研究异面直线所成的角,是将它们转化为两条相交直线所成的角(锐角或直角),基本方法是平移,平移时所选择的点和平行线应具有特殊的位置,或处特殊位置上,求异面直线所成角的一般步骤是:
(1)作图,通过平移,将空间角(两异面直线所在的角)转化为平面角(两条相交直线所成的角),而平移一般有下面三种方法:利用图中已有的平行线平移;过特殊点(如线段的中点或端点)作平行线(常作中位线)平移;补形平移;
(2)证明:证明某平面角就是两异直线所成的角;
(3)计算:通常在三角形中计算.
例5、正方体ABCD—A′B′C′D′的棱长为a,E、F分别是棱A′B′,B′C′的中点,求:
(1)异面直线AD与EF所成角的大小;
(2)异面直线B′C与EF所成角的大小;
(3)异面直线B′D与EF所成角的大小;
(4)异面直线DD′与EF的距离.
[解析]
例6、在正四面体ABCD(四个面是全等的等边三角形的四面体)中,E、F分别是AD、BC的中点,求异面直线AF与CE所成的角.
[解析]
|