|
一、一周知识概述
本周学习了球的概念、性质,球的体积与表面积公式的推导及应用.
球是指与定点的距离等于或小于定长的点的集合.用一个平面截球O,截面是圆面,球心O与截面圆圆心O的连线垂直于截面,设球的半径为R,截面圆半径为R,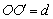 ,则 ,则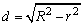 .球的体积与表面积的推导都是采用分割、近似、求和取极限的思路,应理解这种思想方法 . .球的体积与表面积的推导都是采用分割、近似、求和取极限的思路,应理解这种思想方法 .
地球可近似看作球,理解经度、纬度、球面距离等概念,掌握球与其它几何体的接与切等问题的解决方法.
二、重难点剖析
1、球的概念和性质,球的内接、外切问题,球面距离.
(1)球的概念
与定点的距离等于或小于定长的点的集合叫做球体,简称为球.(球与球面是不同的概念)
(2)球的截面性质
1°球心与截面圆圆心的连线垂直于截面.
2°球心到截面的距离d与球的半径R以及截面圆的半径r有如下关系: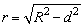 . .
其中,球面被经过球心的平面截得的圆叫做大圆,被不经过球心的面截得的圆叫做小圆.
解决球与多面体接或切问题时,有时也选择球的大圆,用来揭示球与多面体的位置关系.将空间问题转化为平面问题.
在球面上,两点之间的距离,就是经过这两点的大圆在这两点间的一段劣弧的长度.
设球面上两点间的球心角为α(弧度),球半径为R,则球面上两点间的距离为|α|R,所以计算球面距离关键是确定球心角.
(1)当两点在同一经线上,由纬度可确定它们的球心角;
(2)当两点在同一纬线圈上,先求弦长,再由余弦定理求球心角;
(3)当两点经纬度都不同时,用异面直线上两点的距离公式求出弦长,再由余弦定理求球心角.
2、正确理解经纬度对于解决球的问题很重要.
地球上某点的经纬度
当我们把地球看作一个球时,经线就是球面上北极到南极的半个圆,赤道是一个大圆,其余的纬线都是小圆.
某点的经度是指经过这点的经线与地轴确定的半平面与0°经线和地轴确定的半平面所成的二面角度数.
某点的纬度是指经过这点的球半径与赤道面所成角的度数.
如图(1)中,P点的经度是∠AOB的度数或 的度数.如图(2)中,P点的纬度是∠POA的度数或 的度数.如图(2)中,P点的纬度是∠POA的度数或 的度数. 的度数.

三、典型例题讲解
例1、在半径等于25cm的球内有一个截面,它的面积是49πcm2,求球心到这个截面的距离。
[解析]
例2、设地球的半径为R,在北纬45°圈上有两个点A、B,A在西经40°,B在东经50°,求A、B两点间纬线圈的弧长及A、B两点间的球面距离.
[解析]
例3、正三棱锥有一个半径为R的内切球,求这样的三棱锥体积的最小值.
[解析]
例4、如图,正四棱锥S-ABCD内接于球O(正四棱锥的所有顶点都在球面上),底面边长为a,侧棱与底面成角α,求球O的体积。
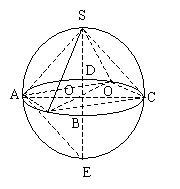
[解析]
|