|
一、一周知识概述
本周首先学习的内容是曲线和方程,要理解曲线的方程和方程的曲线的定义,掌握求曲线的方程的步骤,注意培养同学们全面分析问题的能力,强化数形转换的思想方法,会求两曲线的交点。
在学习圆的方程中,我们学习到如何利用曲线的方程和方程的曲线的关系及求曲线方程的“五步法”,推导出圆的标准方程,进而推导出圆的一般方程;然后利用向量知识和三角函数的定义推导出圆的参数方程.在这一周的学习过程中,同学们可以体验到圆的三种方程形式间的互化及它们在应用中的优缺点,也能体会到利用圆的三种不同的方程形式来处理直线与圆的位置关系,圆与圆的位置关系,求圆的切线方程,求轨迹问题及求最值问题等的不同.同时,通过本周课堂内外的例、习题的讲解与学习,同学们应该能熟练地掌握圆的三种方程形式的灵活运用,并体会到解析几何中的一种很重要的数学思想——数形结合的思想,及待定系数法等.
二、重难点知识归纳总结
学习重点
1、对曲线的方程、方程的曲线的定义的理解。一般地,如果曲线C上的点与二元一次方程F(x,y)=0的实数解建立如下关系:
①曲线上的点的坐标,都是这个方程的解;
②以这个方程的解为坐标的点都是曲线上的点.
那么,这个方程叫做曲线的方程,这条曲线叫做方程的曲线.
2、求曲线的方程
归纳一下课本中的例习题,可以总结出求曲线的方程的五个步骤:
(1)建立适当的直角坐标系,用(x,y)表示曲线上任意点M的坐标;
(2)写出适合条件P的点M的集合P={M|P(M)};
(3)用坐标表示条件P(M),列出方程f(x、y)=0;
(4)化方程f(x,y)=0为最简形式;
(5)证明已化简后的方程的解为坐标的点都是曲线上的点.
注意:除个别情况外,化简过程都是同解变形过程,步骤(5)可省略不写,如有特殊情况,可适当予以说明。另外,根据情况,也可以省略步骤(2),直接列出曲线方程.
3、求曲线的交点
两条曲线有交点的充要条件是它们的方程所组成的方程组有实数解,可见求曲线的交点问题就是求上述方程组的实数解.
如果C1、C2的方程分别为f1(x,y)=0,f2(x,y)=0,点P的坐标为(x1,y1),则
P是C1、C2的交点
4、圆的三种方程形式:
标准方程:x2+y2=r2,(x-a)2+(y-b)2=r2
一般方程:x2+y2+Dx+Ey+F=0(D2+E2-4F>0)
参数方程: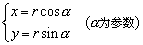
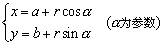
5、根据已知条件利用待定系数法建立圆的标准方程、一般方程、及参数方程.会进行圆的三种形式间的互化,如会由圆的一般方程求出圆的圆心坐标及半径.
一般地,如果已知条件给出圆心坐标(或容易求出)和半径r(或容易求出),或需利用圆心的坐标或半径列方程组的问题,一般采用圆的标准方程较好;如果已知圆过某些定点(一般地三个),一般采用圆的一般方程较好,虽然其中二者都是采取待定系数法,但用一般方程得到的方程组为三元一次方程组,若用标准方程,则得到的是三元二次方程组,解时较繁;如果要求动点轨迹的问题,一般采用参数方程形式较好,但其中“消参”有时较困难.
具体采用哪一种方程形式,要视具体情况而定.
学习难点:
1、是准确理解曲线的方程、方程的曲线的定义。在定义中第①条表示曲线具有纯粹性,即曲线上所有的点都适合这个条件,而毫无例外;第②条说明曲线具有完备性,阐明适合条件的所有点都在曲线上,而毫无遗漏。
曲线与方程建立了严格的对应关系后,两者就成为同一运动规律在“形”和“数”这两个不同方面的反映,曲线的性质完全地反映在它的方程上,方程的性质,又反映在它的曲线上,因此,我们就可以通过方程为来研究曲线,也可以利用曲线研究方程。
2、准确地求出曲线的方程。
要准确地求出曲线方程应注意以下几点:
(1)全面准确理解题意,弄清已知和未知,发现已知和未知的关系;
(2)合理的进行数学语言之间的转换,通过审题画出必要的图形或示意图,根据已知和未知关系进行数学式子或关系的等价转换;
(3)认真挖掘问题中的隐含条件;
(4)注意解题过程中的信息反馈,作出恰当的处理。
求曲线的方程一般有三种方法:
第一种是“直译法”,用于求一般的曲线方程;
第二种是“坐标转移法”,通常用于动点在已知曲线上,而所求点与动点的位置有关;
第三种是“交轨法”,常用于求两直线交点的轨迹,特点是整体消元。
3、选择合适方程形式来处理与圆有关的问题,这一难点也是本周学习中的重点.
由于圆的方程形式相对较多,涉及圆的问题也较多,形式也各不相同,因此合理选择方程形式较难.我们克服难点的方法就是“多练”,从“练”中悟出各种形式的优缺点,从“练”中寻求一般规律.
4、运用平面几何中一些图形性质,简化计算,从而达到简单处理问题的目的.例如:教材P80例6中,教材采用参数方程求解,其实,我们可以利用平面几何图形性质,M为AP的中点,若我们作出OA的中点N,则MN为△OPA的中位线,则 ,所以将问题转化成求一点到定点N(6,0)的距离等于定长2的点的轨迹问题,然后利用圆的定义很容易得到M的轨迹为以(6,0)为圆心,半径为2的圆. ,所以将问题转化成求一点到定点N(6,0)的距离等于定长2的点的轨迹问题,然后利用圆的定义很容易得到M的轨迹为以(6,0)为圆心,半径为2的圆.
其中参数方程的应用中“消参”也是一个难点,这一难点的克服,一方面积累一些消参方法,如:代入消参法,加减消参法,运用三角函数消参法,和运用代数中常见的运算技巧消参法;另一方面,熟练地运用三角函数中的一些变形技巧(积化和差,和差化积,平方相加,平方相减等).
三、典型例题分析
例1、过定点A(a,b)任作两条互相垂直的直线,分别交x,y轴于M,N两点,求线段MN的中点P的轨迹方程.
分析:
求轨迹方程,要充分挖掘图形的几何性质,根据曲线上的点所适合的条件列出等式.此题的切入口是用好条件AM⊥AN,可以根据两直线垂直且斜率存在,则它们的斜率之积为-1建立方程,也可以根据直角三角形斜边上的中线等于斜边的一半建立方程,还可以利用勾股定理建立方程.
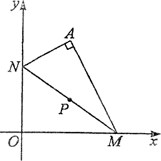
解法1:
如图,设P(x,y),则M(2x,0),N(0,2y).
因为AM⊥AN,则有kAM·kAN=-1,即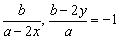 , ,
整理得2ax+2by-a2-b2=0.①
当AM⊥x轴时,kAM不存在,此时P点为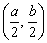 ,坐标满足方程①, ,坐标满足方程①,
因此,方程①就是所求的轨迹方程.(注:垂直如用向量处理则无需讨论)
解法2:
设P(x,y),由题意可得M(2x,0),N(0,2y).
∵△AMN是直角三角形,AP为斜边MN上的中线.
∴|MN|=2|AP|,即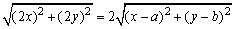 , ,
化简得2ax+2by-a2-b2=0.
解法3:
设P(x,y),由题意可得M(2x,0),N(0,2y).
∵△AMN是直角三角形,由勾股定理得|AM|2+|AN|2=|MN|2,
即(2x-a)2+b2+a2+(2y-b)2=(2x)2+(2y)2,
化简得2ax+2by-a2-b2=0.
解法4:
设P(x,y),连OP.
由△OMN为直角三角形知 , ,
又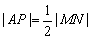 ,∴|OP|=|AP|, ,∴|OP|=|AP|,
即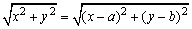 , ,
平方化简得2ax+2by-a2-b2=0.
解法5:
当AM⊥x轴时,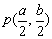
当AM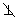 x轴时,直线AM:y-b=k(x-a)∴M x轴时,直线AM:y-b=k(x-a)∴M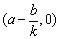 , ,
直线AN: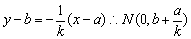 . .
设P(x,y),则
则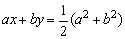 . .
又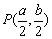 也符合上式,故P的轨迹方程为2ax+2by-a2-b2=0. 也符合上式,故P的轨迹方程为2ax+2by-a2-b2=0.
小结:
解法1通常称为直接法,即根据已知条件直接列出方程.解法2、3、4是运用直角三角形的性质,得出线段长之间的关系,这种方法称为几何法.解法5利用x、y与k的关系求出方程,通常称为参数法.
例2、已知A(2,0),B(-1,2),点C在直线2x+y-3=0上移动,求△ABC重心的轨迹的方程.
分析:
用动点G(x,y)的坐标来表示已知曲线上的相关点A(x0,y0)的坐标,再代入已知曲线方程.
解答:
设△ABC的重心为G(x,y),点C坐标为(x1,y1),
则有2x1+y1-3=0,
由重心坐标公式有 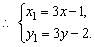
∴ 2(3x-1)+(3y-2)-3=0,即6x+3y-7=0(x≠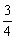 )。 )。
小结:
这种求轨迹方程的方法称为转换法(又称代点法或相关点法),就是用所求动点的坐标x,y来表示已知动点的坐标,并代入已知动点满足的已知曲线的方程.由此即可求得动点坐标x、y之间的关系.所得曲线又称为已知曲线的伴随曲线.
例3、已知线段AA′=2a,直线l垂直平分AAˊ于O,在l上取两点P,P′,使有向线段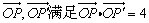 ,求两直线AP,A′P′的交点M的轨迹方程. ,求两直线AP,A′P′的交点M的轨迹方程.
分析:
首先应根据对称性建立直角坐标系.其次,要正确理解有向线段数量的意义.再引进参数(越少越好),刻划P点的纵坐标,则Pˊ点坐标可求,两条动直线方程亦可求.进而消去参数,得所求轨迹方程.
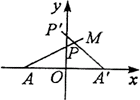
解:
如图,以A Aˊ所在直线为x轴,以A Aˊ的中垂线为y轴建立直角坐标系,
设点P(0,t)(t≠0),则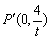 . .
由点斜式得直线AP、AˊPˊ的方程分别为 . .
两式相乘,消去t,得 . .
这就是所求点M的轨迹方程.
小结:
此题仍采用的是参数法.用参数法求轨迹方程,关键有二:一是选参,容易写出动直线方程.二是消参.消参的途径灵活多变,有时从一个方程中解出参数,再代入另一个方程中消参;有时分别从两个方程中解出参数,再消参;有时分别解出x,y,再消参;有时直接或作适当变形后,通过加、减、乘、除,求平方和,求平方差等方法整体消参.
例4、 已知圆与y轴相切,圆心在直线l∶x-3y=0上,且被直线y=x截得的弦长为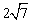 ,求圆的方程. ,求圆的方程.
分析:
本题涉及圆心的坐标,又已知该圆与y轴相切,即易表示出半径,故应用圆的标准方程处理起来较简单.
解:设所求圆的方程为:(x-a)2+(y-b)2=r2,
由题意知a-3b=0 ①,
r=|a| ②
又所求圆的圆心到直线y=x的距离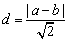 , ,
故由垂径定理和勾股定理得: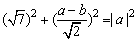 ③ ③
由①②③解得: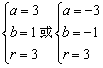
故所求圆的方程为:
(x-3)2+(y-1)2=9,或 (x+3)2+(y+1)2=9.
小结:
1°直线与圆相交,求弦长,或求与弦长有关的问题,利用平面几何的垂径定理往往非常简单.
2°在求圆的方程中,若已知圆心坐标或圆心坐标满足某一方程(如已知圆心在某一直线上),又已知圆的半径的长度或可用与圆心坐标有关的参数表示时,一般常设圆的标准方程形式,利用待定系数法求解.
例5、 求圆x2+y2=r2在定点C(c,0)张直角之弦的中点的轨迹(|c|≠|r|).
分析:
弦的中点取决于两端点的坐标,故可设出弦的两端点的坐标为
 参数,根据轨迹条件建立三个方程,然后消去参数 参数,根据轨迹条件建立三个方程,然后消去参数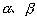 ,即可得轨迹方程. ,即可得轨迹方程.
本题解法较多,在此,综合三种解法,旨在广开思路,多方位,多角度思考问题,提高发散思维能力,提高分析解决问题能力.
解答:
方法一: 设弦的两端点坐标分别为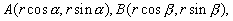
AB的中点P的坐标为(x,y),则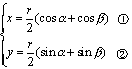
∵ AC⊥BC,
1°当AC,BC所在直线的斜率都存在时有
变形整理,得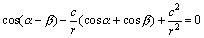 ③ ③
下面从①②③中消去参数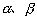 . .
①2+②2 得
即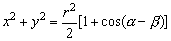
∴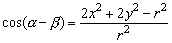 ④ ④
将④①代入③,得:2(x2+y2)-2cx+c2-r2=0
即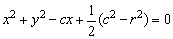 ⑤ ⑤
2°当AC或BC的所在直线的斜率不存在时,即
①当AC斜率不存在,此时 , ,
AB中点坐标为 同样适合方程⑤. 同样适合方程⑤.
②同理,当AB斜率不存在,AB中点坐标也适合方程 ⑤,
故AB中点在方程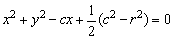 所表示的图形上. 所表示的图形上.
下面来讨论方程⑤表示的图形.
方程⑤可变形为: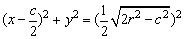
1°当2r2>c2时,轨迹是圆,它是在已知圆内部的一段弧
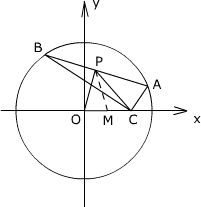
2°当2r2=c2时,轨迹为一点
3°当2r2<c2时,轨迹不存在.
方法二:下面用几何方法求解.
令p(x,y)为轨迹上任意一点,如图
∵ AC⊥BC, P为AB的中点,故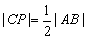 , ,
设M为OC的中点,则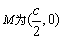 , ,
有2(|MP|2+|OM|2)=|OP|2+|CP|2=r2,

以下讨论点的轨迹问题同方法一.
(其中或利用直角三角形知识解决,∵ OP⊥AB,
∴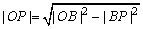 ,又|BP|=|PC|,|OB|=r, ,又|BP|=|PC|,|OB|=r,
∴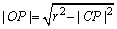 ,再利用两点间距离公式求解.) ,再利用两点间距离公式求解.)
方法三:
下面运用直线的参数方程求解,有兴趣的同学在自学了教材P55直线的参数方程后可选择学习.
设P(x0,y0)为轨迹上任一点,令|cp|=t,直线AB的倾斜角为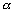 , ,
则A、B两点坐标分别为:
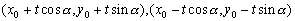
∴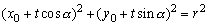 ① ①
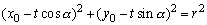 ② ②
t2=(x0-c)2+y02 ③
①+②得2x02+2y02+2t2=2r2
即x02+y02+t2=r2 ④
③代入④得, x02+y02+(x0-c)2+y02-r2=0
即2(x02+y02)-2cx0+c2-r2=0
以(x,y)代(x0,y0)即可得所求轨迹方程:
2(x2+y2)-2cx+c2-r2=0,
以下解法同方法一.
小结:
1°利用参数方程解决求轨迹问题较利用圆的标准方程,一般方程简单,很容易得到要求动点的轨迹的参数方程,但其中要得一般方程,“消参”是难点,应注意常用的消参方法.
2°在解决与圆有关的弦长等问题时,利用平面几何知识求解,常使问题解得简单明了.
例6、如果实数x,y满足x2-y2-4x+1=0,求:
(1)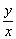 的最大值; 的最大值;
(2)y-x的最小值.
分析:
x2+y2-4x+1=0 表示以(2,0)为圆心,半径为 的圆, 的圆, 表示点(x,y)与原点连线的斜率.问题(1)实质是求圆上的点与原点的连线的斜率的最大值.问题(2)中,
设y-x=b,则y=x+b,可知b是斜率为1的直线在y轴上的截距,于是问题(2)实质上是求斜率为1的直线与已知圆有公共点时直线的纵截距的最小值. 表示点(x,y)与原点连线的斜率.问题(1)实质是求圆上的点与原点的连线的斜率的最大值.问题(2)中,
设y-x=b,则y=x+b,可知b是斜率为1的直线在y轴上的截距,于是问题(2)实质上是求斜率为1的直线与已知圆有公共点时直线的纵截距的最小值.
解答:
(1)设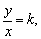 得y=kx,所以k为过原点的直线的斜率,又x2+y2-4x+1=0表示以(2,0)为圆心,半径为 得y=kx,所以k为过原点的直线的斜率,又x2+y2-4x+1=0表示以(2,0)为圆心,半径为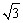 的圆,如图: 的圆,如图:

当直线y=kx与已知圆相切且切点在第一象限时,k最大,此时:
|OP|= ,
|OC|=2, ,
|OC|=2,
∴Rt△POC中,∠POC=60°,k=tan60°=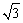 , ,
∴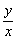 的最大值为 的最大值为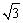 . .
(2)设y-x=b,即为直线y=x+b,b为直线在y轴上的截距,如图所示.
当直线y=x+b与圆有公共点时,当且仅当与圆相切,且切点在第四象限时b最小,此时,圆心(2,0)到直线的距离为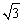 , ,
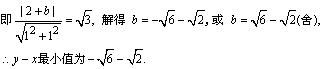
|