|
一、一周知识概述
本周学习内容是高二上数学第八章的第三节和第四节,即§8.3双曲线及其标准方程,以及§8.4双曲线的简单几何性质;共用时五个课时.具体安排为§8.3两个课时,§8.4三个课时.
双曲线的定义、标准方程、简单几何性质与椭圆类似,所以本周内容在数学思想和方法上没有新内容,学习中可与椭圆的相关知识进行对比,注意它们的联系和区别.在本周的学习中,我们学习了双曲线的定义,标准方程的推导,并能根据条件确定双曲线的标准方程,同时通过类比椭圆几何性质的研究方法.同学们可以自主探究双曲线的范围、对称性、顶点、离心率等几何性质,提高了类比分析归纳的能力.
二、重、难点知识的归纳与解析
1、本周学习与研究中的两个重点
第一个重点是§8.3中的双曲线的定义与标准方程.
双曲线的定义是,平面内与两个定点F1、F2的距离的差的绝对值等于常数(小于|F1F2|)的点的轨迹叫做双曲线.
定义中“小于|F1F2|”这一限制条件十分重要,不可去掉.若定义中常数改为等于|F1F2|,此时动点轨迹是以F1、F2为端点的两条射线;若定义中常数改为大于|F1F2|,此时动点轨迹不存在.
如果双曲线的焦点在x轴上,标准方程为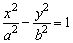 (a>0,b>0) (a>0,b>0)
如果双曲线的焦点在y轴上,标准方程为 (a>0,b>0). (a>0,b>0).
双曲线标准方程中a>0,b>0,但a不一定大于b.如果x2的系数是正的,那么焦点在x轴上,如果y2的系数是正的,那么焦点在y轴上,有别于椭圆通过比较分母的大小来判定焦点的位置.
第二个重点是双曲线的几何性质及其运用.
双曲线的简单几何性质如下表所示:
标准方程 |
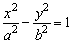 (a>0,b>0) (a>0,b>0)
|
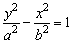 (a>0,b>0) (a>0,b>0)
|
图形 |
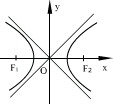
|

|
范围 |
|x|≥a,y∈R |
|y|≥a,x∈R |
对称性 |
对称轴:x轴、y轴,对称中心:原点 |
离心率 |
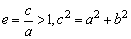
|
顶点 |
(-a,0)(a,0) |
(0,-a),(0,a) |
焦点 |
(-c,0)(c,0) |
(0,-c)(0,c) |
准线 |

|

|
渐近线 |
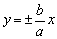
|

|
双曲线中的“六线”:两条对称轴、两条准线、两条渐近线;
“四点”:两个顶点、两个焦点。注意它们的位置关系及其相互间距离。
2、本周学习与研究中的两个难点
第一个难点是双曲线标准方程的推导.
与建立椭圆的标准方程一样,我们仍从双曲线的定义出发,采用坐标法,按照求曲线方程的基本步骤,推导出了双曲线的标准方程,带根式的方程的化简是我们要注意的问题.
第二个难点是双曲线渐近线方程的导出和论证.
对圆锥曲线来说,渐近线是双曲线特有的性质.在研究双曲线范围时,由双曲线标准方程可解出:
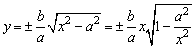 , ,
当 x→+∞时,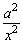 →0, →0,
双曲线 与直线 与直线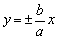 无限接近,使我们猜想直线 无限接近,使我们猜想直线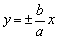 为双曲线的渐近线.证明时,只要考虑双曲线在第一象限,即证当x无限增大时,双曲线上的点M(x,y)到直线 为双曲线的渐近线.证明时,只要考虑双曲线在第一象限,即证当x无限增大时,双曲线上的点M(x,y)到直线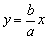 的距离趋近于0即可. 的距离趋近于0即可.
三、例题点评
例1、已知方程 表示的图形是 表示的图形是
(1)圆 (2)椭圆 (3)双曲线
分别求出k的取值范围.
[解析]
例2、求渐近线方程为3x±4y=0,焦点为椭圆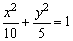 的一对顶点的双曲线方程. 的一对顶点的双曲线方程.
[解析]
例3、经过双曲线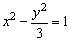 的右焦点F2作倾斜角为30°的弦AB, 的右焦点F2作倾斜角为30°的弦AB,
(1)求|AB|.
(2)F1是双曲线的左焦点,求△F1AB的周长.
[解析]
例4、已知双曲线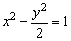 . .
(1)过点A(2,1)的直线l与所给双曲线交于两点P1、P2,求线段P1P2中点P的轨迹方程;
(2)过点B(1,1)能否作直线m,使m与所给双曲线交于两点Q1、Q2,且点B是线段Q1Q2的中点?这样的直线若存在,求出方程;若不存在,说明理由?
[解析]
|