|
一、一周知识概述
本周学习了椭圆的第一定义,两种形式的标准方程及其推导过程,标准方程的求法;几个简单的几何性质:范围、对称性、顶点、离心率.椭圆的第二定义,椭圆的参数方程,直线与椭圆等.
二、重难点知识选讲
1、椭圆第一定义:平面内与两定点F1、F2的距离的和等于常数2a(2a>|F1F2|)的点的轨迹叫做椭圆.定点F1、F2叫做椭圆的焦点,|F1F2|(即两焦点的距离)叫做椭圆的焦距.
集合语言叙述为:点集P={M||MF1|+|MF2|=2a,2a>|F1F2|},其中两定点F1、F2叫做椭圆的焦点,两焦点的距离叫椭圆焦距.
例1、命题甲:动点P到两定点A、B的距离之和|PA|+|PB|=2a(a>0,a为常数);乙命题:P点的轨迹是椭圆,且A、B是椭圆的焦点,则命题甲是命题乙的( )
A.充分不必要条件
B.必要不充分条件
C.充要条件
D.既不充分又不必要条件
[解析]
2、标准方程和求法
(1)焦点在x轴上的椭圆的标准方程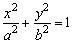 (a>b>0); (a>b>0);
(2)焦点在y轴上的椭圆的标准方程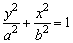 (a>b>0). (a>b>0).
3、方程Ax2+By2=C表示椭圆的条件是A、B、C同号,且A≠B,可化为标准形式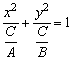 . .
例2、求椭圆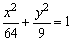 的焦点坐标,若AB为过左焦点F1的弦,则△F2AB(F2为右焦点)的周长为多少? 的焦点坐标,若AB为过左焦点F1的弦,则△F2AB(F2为右焦点)的周长为多少?
[解析]
例3、求椭圆mx2+ny2+mn=0(m<n<0)的焦点坐标.
[解析]
4、求标准方程
(1)待定系数法
首先确定焦点所在轴,设出对应的标准方程形式,再利用条件求出a,b的值.
例4、根据下列条件,分别求出椭圆的标准方程.
(1)焦点坐标为(0,-4),(0,4),a=5;
(2)a=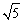 ,c=1; ,c=1;
(3)经过两点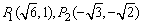 . .
[解析]
(2)定义法
例5、已知⊙M:(x+1)2+y2=16及点A(1,0),C为⊙M上任意一点,求AC的垂直平分线l与线段CM的交点P的轨迹方程.
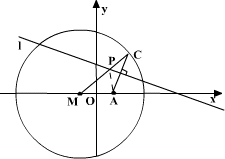
[解析]
5、椭圆的简单几何性质:(研究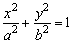 (a>b>0)). (a>b>0)).
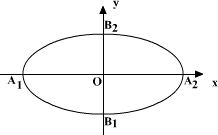
(1)范围x∈[-a,a],y∈[-b,b];
(2)对称性:关于x轴,y轴和原点都对称,若符合其中两种对称,则必符合另一种对称;
(3)顶点:
A1(-a,0),A2(a,0),B1(0,-b),B2(0,b).A1A2叫长轴,B1B2叫短轴.
(4)离心率: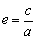
e是刻画椭圆的圆扁程度的量,e→1时,椭圆越扁e→0时,椭圆越接近圆.
例6、已知椭圆x2+(m+3)y2=m的离心率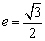 时,求m的值及椭圆的长轴和短轴的长、焦点坐标. 时,求m的值及椭圆的长轴和短轴的长、焦点坐标.
[解析]
6、椭圆的第二定义
平面内与定点F的距离和它到直线l的距离的比是小于1的正常数e的点的轨迹叫椭圆.定点F为焦点,定直线l称为相应的准线,且左焦点与左准线对应,右焦点与右准线对应,常数e为椭圆的离心率.
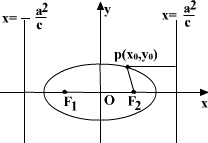
如图,对于椭圆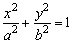 (a>b>0),相对应于焦点F2(c,0)的准线方程是 (a>b>0),相对应于焦点F2(c,0)的准线方程是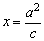 ;相对应于F1(-c,0)的准线方程是 ;相对应于F1(-c,0)的准线方程是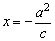 ,由第二定义易得:当P为椭圆上一点时,|PF1|=a+ex0,|PF2|=a-ex0,习惯上称线段PF1,PF2为焦半径. ,由第二定义易得:当P为椭圆上一点时,|PF1|=a+ex0,|PF2|=a-ex0,习惯上称线段PF1,PF2为焦半径.
例7、椭圆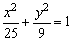 上有一点P,它到左准线的距离等于2.5,那么,P到右焦点的距离为(
) 上有一点P,它到左准线的距离等于2.5,那么,P到右焦点的距离为(
)
A.8 B. C. C.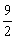 D. D.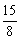
[解析]
7、椭圆的参数方程
若椭圆方程为 (a>b>0),则其参数方程为 (a>b>0),则其参数方程为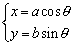 (θ为参数).我们常利用椭圆的参数方程解决与椭圆上动点有关的问题. (θ为参数).我们常利用椭圆的参数方程解决与椭圆上动点有关的问题.
例8、已知点P在圆O′: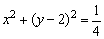 上移动,点Q在椭圆x2+4y2=4上移动,求|PQ|的最大值及相应的点Q的坐标. 上移动,点Q在椭圆x2+4y2=4上移动,求|PQ|的最大值及相应的点Q的坐标.
[解析]
3、直线与椭圆
有关直线与椭圆的综合问题,应该说既是这章的重点,又是这一章的难点,处理方法是将直线方程与椭圆方程联系,消去y(或x),得到关于x(或y)的一元二次方程.△>0时,直线与椭圆有两个公共点,且两点间距离为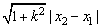 (k为直线斜率,x1、x2为两公共点坐标).若将两点坐标分别代入椭圆方程,并两式相减得 (k为直线斜率,x1、x2为两公共点坐标).若将两点坐标分别代入椭圆方程,并两式相减得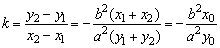 ((x0,y0)为两公共点的中点),这就是我们常说的点差法. ((x0,y0)为两公共点的中点),这就是我们常说的点差法.
△=0时,直线与椭圆有且只有一个公共点;△<0时,直线与椭圆无公共点.
例9、设x,y∈R,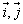 为直角坐标平面内x,y轴正方向上的单位向量,若向量 为直角坐标平面内x,y轴正方向上的单位向量,若向量
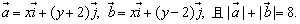
(1)求点M(x,y)的轨迹C的方程;
(2)过点(0,3)作直线l与曲线C交于A、B两点,设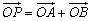 ,是否存在这样的直线l,使得四边形OAPB为矩形?若存在,求出直线l的方程;若不存在,试说明理由. ,是否存在这样的直线l,使得四边形OAPB为矩形?若存在,求出直线l的方程;若不存在,试说明理由.
[解析]
|