|
一、一周知识概述
立体几何的学习是平面几何学习的延续和发展,空间图形与平面图形之间存在着密切的联系.本单元学习的主要目的就是探讨二者之间的关系,从而解决多面体不共面的两点的最短距离及空间图形中点、线、面的位置关系等一系列问题,培养大家的空间想象能力,安排两到三个课时.
二、重、难点知识归纳与剖析
本单元学习的重点、难点是会解决图形的展开与折叠问题.
将空间问题转化为平面问题是一种重要和常用的方法.例如推导圆柱、圆锥的侧面积公式时,就是将其侧面展开,转化为矩形、扇形而得到解决的,这就是应用了“以直代曲”的方法,对于多面体不共面的两点的最短距离均可采用此法.
将平面图形折叠成立体图形,处理这类问题时应注意折叠前、后哪些量发生了改变,哪些没有发生改变.特别应注意寻找折叠前后的那些没有发生变化的关系和没有变化的量.
三、例题点评
例1、正三棱柱ABC—A1B1C1中,各棱长均为2,M为AA1中点,N为BC中点,则在棱柱的表面上从点M到点N的最短距离是多少?并求之.
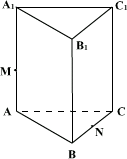
[解析]
例2、设正三棱锥P—ABC的底面边长为a,侧棱长为2a,过A作与PB、PC分别交于D、E的截面.
(1)求截面三角形ADE的周长的最小值;
(2)求截面三角形ADE周长最小时的截面面积.
[解析]
例3、△BCD内接于直角梯形A1A2A3D,已知沿△BCD三边把△A1BD、△A2BC、△A3CD翻折上去,恰好使A1,A2,A3重合成A.
(1)求证:AB⊥CD;
(2)若A1D=10,A1A2=8,求二面角A—CD—B的正切值.
[解析]
例4、等边三角形ABC的边长为a,沿平行于BC的线段PQ折起,使平面APQ⊥平面PBCQ,设点A到直线PQ的距离为x,AB的长为d.
(1)x为何值时,d2取得最小值,最小值是多少;
(2)∠BAC=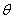 ,求cos ,求cos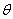 的最小值. 的最小值.
[解析]
|