直线的倾斜角和斜率的概念是本节的重点,直线方程的点斜式是求直线方程的基本形式,是求直线方程的重点.
斜率概念的学习和过两点的直线的斜率公式的建立,以及依据所给条件的异同与特点,合理选取直线方程的不同形式是本节的难点.
(1)、直线的方程与方程的直线
以一个方程的解为坐标的点都是某条直线上的点,且这条直线上的点的坐标都是这个方程的解.这时,这个方程叫这条直线的方程,这条直线叫做这个方程的直线.
在平面解析几何里研究直线时,就是利用直线与方程这种关系建立直线的方程,并通过方程来研究直线的有关问题.
(2)、直线的倾斜角与斜率
在平面直角坐标系中,对于一条与x轴相交的直线,如果把x轴绕着交点按逆时针方向旋转到和直线重合时所转的最小正角为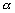 ,则
,则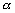 就叫做直线的倾斜角;当直线和x轴平行或重合时,规定此时直线的倾斜角为0°,因此,倾斜角的范围是0°≤
就叫做直线的倾斜角;当直线和x轴平行或重合时,规定此时直线的倾斜角为0°,因此,倾斜角的范围是0°≤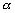 <180°
<180°
倾斜角是一个几何概念,直观的描述了直线对x轴正方向的倾斜程度.
倾斜角不是90°的直线,它的倾斜角的正切叫做这条直线的斜率.直线的斜率常用k表示,即k=tan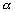 ,直线的倾斜角为90°时,没有斜率.
,直线的倾斜角为90°时,没有斜率.
(3)、直线的斜率公式
在平面坐标系内,两点P1(x1,y1),P2(x2,y2)决定一条直线,当直线P1P2的倾斜角不为90°时,它的斜率公式为: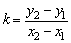 .
.
斜率公式与两点的顺序无关,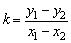 .
.
若y2=y1, x2≠x1,则直线P1P2与x轴平行或重合,k=0;若y2≠y1,x2=x1,则直线的倾斜角为90°,斜率不存在.
(4)、直线方程的点斜式
若直线l经过点P1(x1,y1),且斜率为k,则l的方程为:y-y1=k(x-x1).
若l过P0(x0,y0)且与x轴平行或重合,则k=0,由点斜式有y=y0.
若l过P0(x0,y0)且与x轴垂直,则l的倾斜角为90°,没有斜率,此时直线方程不能用点斜式表示,应为x=x0.
(5)、直线方程的斜截式
若已知直线l的斜率为k,与y轴的交点为P(0,b), 代入点斜式有:y-b=k(x-0),即y=kx+b.b是直线l在y轴上的截距,截距可以是任一实数,而距离只能是非负数.
求截距的方法:在直线l的方程中,令x=0,解出y值,可得直线l在y轴上的截距;令y=0,解出x,即得直线在x轴上的截距.
(6)、直线方程的两点式
已知直线l经过P1(x1,y1),P2(x2,y2),(x1≠x2),则直线l 的方程为: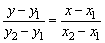 .
.
当直线l没有斜率(x1=x2)或斜率为0(y1=y2)时不能用两点式计算.
(7)、直线方程的截距式
已知直线l与x轴交点为(a,o),与y轴交点为(0,b),其中ab≠0,则直线l的方程为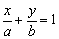 .
.
已知l在坐标轴上的截距且不为零时,用截距式表示方程可以快速准确的画出直线来.
(8)、直线方程的一般式
直线方程的四种形式不能表示所有的直线,都有特殊情形需要单独讨论,可以用二元一次方程统一起来.
①直线的方程都可以写成关于x,y的二元一次方程.
证明:在平面直角坐标系中,每一条直线都有唯一的倾斜角 与之对应.
与之对应.
i)当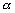 ≠90°时,方程可以写成y=kx+b的形式,即:kx-y+b=0;
≠90°时,方程可以写成y=kx+b的形式,即:kx-y+b=0;
ii) 当 =90°时,它的方程可以写成x=x1的形式,即:x+0·y-x1=0.
=90°时,它的方程可以写成x=x1的形式,即:x+0·y-x1=0.
∴ 直线的方程可以写成关于x,y的二元一次方程的形式.
②任何关于x,y的二元一次方程都表示一条直线.
证明:关于x,y的二元一次方程的一般形式是
Ax+By+C=0 (其中A,B不同时为0).
i) 当B≠0时,可化为 ,它表示斜率为
,它表示斜率为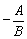 ,在y轴上的截距为
,在y轴上的截距为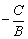 的一条直线.
的一条直线.
ii)当B=0时,A≠0,有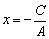 ,它可以表示一条与y轴平行或重合的直线.
,它可以表示一条与y轴平行或重合的直线.
∴ 关于x,y的二元一次方程表示一条直线.
因此,我们把方程Ax+By+C=0(A,B不同时为0)叫做直线方程的一般形式.
直线方程的其它形式都可以化为一般式;在满足某些条件时,直线方程的一般式也可以化为其它形式.
2、本周所学内容的难点.
直线的方程和方程的直线的理解,斜率公式的建立,直线的方程的几种形式以及它们之间的相互转化,每一种方程所对应的直线的特征及要求.由给定直线上的点或斜率写出直线的方程.