|
一、一周知识概述
本周学习内容是高二(下)数学第九章的第三节,即§9.3直线和平面平行及§9.4.直线和平面垂直的前3小节.在本周的课本学习中,我们学习两个知识点,直线和平面平行,直线和平面垂直.通过这周的学习,我们理解了直线和平面平行,直线和平面垂直等基本概念;学会如何判定直线和平面平行,直线和平面垂直,同时学到了直线和平面平行,直线和平面垂直的性质.
二、重难点知识讲解
1、直线和平面平行的判定定理
如果平面外的一条直线和这个平面内的一条直线平行,那么这条直线和这个平面平行.
判定直线和平面平行的主要依据是判定定理,它是通过线线平行来判定线面平行,这里所说的线是指平面外的一条直线和平面内的一条直线.这个定理用符号语言来表示,即若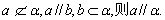 在应用该定理证明线面平行时,这三个条件缺一不可. 在应用该定理证明线面平行时,这三个条件缺一不可.
2、直线和平面平行的性质定理
如果一条直线和一个平面平行,经过这条直线的平面和这个平面相交,那么这条直线和交线平行.
线面平行的性质定理是由线面平行推出线线平行.这里的线线是指与平面平行的一条直线和过这条直线的平面与已知平面的交线,这个定理用符号语言来表示,用 则a∥b.在应用该定理时,要防止出现“一条直线平行于一个平面就平行于这个平面内的一切直线”的错误. 则a∥b.在应用该定理时,要防止出现“一条直线平行于一个平面就平行于这个平面内的一切直线”的错误.
3、直线与平面垂直的判定定理
直线和平面垂直的判定定理是判定直线和平面垂直的理论依据,它可以将要证线面垂直问题,转化成证线线垂直问题.定理中的三个条件:两个线线垂直和一个相交条件推得结论.三个条件缺一不可,尤其是最后一个——两条相交直线这一条件极易忽视.如命题1:如果一条直线垂直于平面内的两条直线,那么这条直线垂直于这个平面;命题2:如果一条直线垂直于平面内的无数条直线,那么这条直线垂直于这个平面.以上两个命题都是错误的,因为对于这两个命题,都没有体现出两直线相交这一特性,无数条直线可以是一簇平行线,并不一定具备有两条相交直线和已知直线垂直,因此,也就不一定得出这一直线垂直于这个平面这一结论.要判定一条已知直线和一个平面是否垂直,取决于在这个平面内能否找出两条相交直线和已知直线垂直,至于这两条相交直线是否和已知直线有公共点,这是无关紧要的.
4、直线与平面垂直的性质定理
如果两条直线同垂直于一个平面,那么这两条直线平行.
一条直线和一个平面平行时,这条直线上任意一点到这个平面的距离,叫做这条直线到这个平面的距离.
三、例题讲解
例1、已知有公共边AB的两个全等的矩形ABCD和ABEF不在同一平面内,P、Q分别是对角线AE、BD上的点,且AP=DQ,求证:PQ∥平面CBE.
分析:
显然,直线PQ在平面CBE外,因此要证明PQ∥平面CBE,只需要在平面CBE内找一条直线,使PQ平行于这条直线.
证明1:作PM∥AB交BE于点M,作QN∥AB交于BC于点N,如图.
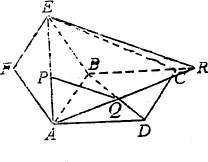
则PM∥QN,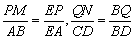 . .
∵ EA=BD,AP=DQ,∴ EP=BQ.
又AB=CD,∴ PM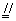 QN .∴四边形PMNQ是平行四边形, QN .∴四边形PMNQ是平行四边形,
∴ PQ∥MN.
又PQ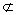 平面CBE,ER 平面CBE,ER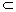 平面CBE,∴ PQ∥平面CBE. 平面CBE,∴ PQ∥平面CBE.
证明2:连结AQ并延长交直线BC于R,连结ER,如图.

∵ AD∥BR,∴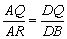 ,∵ DQ=AP,DB=AE, ,∵ DQ=AP,DB=AE,
∴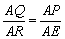 ,∴ PQ∥ER, ,∴ PQ∥ER,
又PQ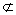 平面CBE,ER 平面CBE,ER 平面CBE,∴ PQ∥平面CBE. 平面CBE,∴ PQ∥平面CBE.
例2、证明:一直线与两相交平面都平行,则这条直线与这两个相交平面的交线平行.
分析:
证明线线平行,往往通过线面平行来证明.已知中有线面平行,可利用线面平行的性质定理将此平行关系转化为线线平行,而利用线面平行的性质定理就必须找出或作出辅助平面;也可利用同一证法或反证法证明.本题应先写出已知、求证、作好图.
已知:a∥α,a∥β,α∩β=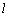 . .
求证:a∥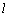 . .
证法一:如图,过a作平面γ交平面α于b,

∵ a∥α,∴ a∥b.
同样,过a作平面γ交平面β于c.
∵ a∥β,∴ a∥c. ∴ b∥c.
又∵ b β,且c β,且c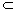 β,∴ b∥β. β,∴ b∥β.
又平面α经过b交β于直线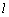 ,∴ b∥ ,∴ b∥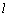 . .
又a∥b,∴ a∥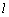 . .
证法二:
如图,在直线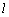 上任取一点A,过点A和a作平面和α相交于直线 上任取一点A,过点A和a作平面和α相交于直线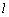 1,和β相交于直线 1,和β相交于直线 2. 2.
∵ a∥α,∴ a∥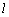 1, 1,
又a∥β,∴ a∥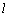 2, 2,
但过一点只能作一条直线与另一条直线平行,
∴ 直线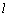 1与直线 1与直线 2重合. 2重合.
又∵ 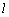 1 1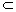 α, α,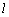 2 2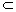 β, β,
∴ 直线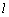 1, 1, 2重合于直线 2重合于直线 ,∴ α∥ ,∴ α∥ . .
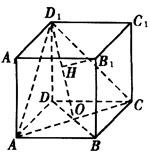
例3、如图所示,正方形ABCD-A1B1C1D1中O是底面ABCD的中心,B1H⊥D1O,H为垂足,求证:B1H⊥平面AD1C.
分析:
要证明B1H⊥平面AD1C,已知B1H⊥D1O,只需证明平面AD1C内与D1O相交的另一直线AC⊥B1H即可,改证AC⊥B1H,只需证AC垂直于B1H所在的平面BD1即可.
证明:
连B1D1,∵B1B⊥AB,B1B⊥BC,∴B1B⊥平面AC,∴B1B⊥AC.
又AC⊥BD,∴AC⊥平面BD1,又B1H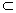 平面BD1,∴AC⊥B1H. 平面BD1,∴AC⊥B1H.
又B1H⊥D1O,∴B1H⊥平面AD1C.
点评:
本题所采用的思维方法是分析法.可先由结论出发判定要证什么,需证什么,然后再结合已知进一步推导.在解题的过程中,常常是线面垂直的判定定理和定义反复交替使用,所以书写步骤要准确、严谨、富有逻辑性.
例3、求证:过一点和一条直线垂直的平面只有一个.
分析:
教材上仅仅以一句话就说明:过空间一点有且仅有一个平面和已知直线垂直,有且仅有一条直线和已知平面垂直,在此证明平面的唯一性.一般采用反证法来证明唯一性.先将其改写成已知、求证的形式.
解答:已知:点A和直线a(如图),
求证:过点A和直线a垂直的平面只有一个.
证明:
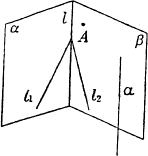
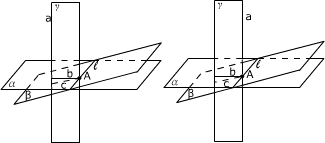
不论点A是否在直线a上(如图),设过点A与直线a垂直的平面为α.如果还有一个平面β过点A且与直线a垂直,且α∩β=l.设过点A和直线a的平面为γ,且α∩γ=b, β∩γ=c,
∵ a⊥α,a⊥β, ∴ a⊥b,a⊥c.
这样在同一平面γ内,过一点A就有两条直线b,c都与a垂直,这是不可能的. 所以,过点A和直线a垂直的平面只有一个.
点评:理解直线和平面垂直的关键是直线与平面内的任意一条直线都垂直.
|