一、一周知识概述

　　本周继续研究直线和平面的有关问题，主要学习直线和平面斜交的有关知识，即直线和平面所成的角和三垂线定理．

二、重难点知识讲解

1、斜线在平面内的射影

　　（1）过斜线上斜足以外的一点向平面引垂线，过垂足和斜足的直线叫做斜线在这个平面内的射影．

　　特别地：

　　①当直线和平面垂直的时候，直线在平面内的射影是一个点.

　　②当直线和平面平行的时候，直线在平面内的射影是一条和该直线平行的一条直线．

　　射影长定理：从平面外一点向这个平面所引的垂线段和斜线段中

　　①射影相等的两条斜线段相等，射影较长的斜线段也较长，

　　②相等的斜线段的射影相等，较长的斜线段的射影也较长，

　　③垂线段比任何一条斜线段都短．

例1、直角三角形ABC的斜边BC在平面α内，顶点A在平面α外，则△ABC的两条直角边在平面α内的射影与斜边组成的图形只能是（　　）

　A．一条线段　　　　　　　　　　 B．一个锐角三角形

　C．一个钝角三角形　　　　　　　 D．一条线段或一个钝角三角形

[解答]

2、直线和平面所成的角

　　（1）直线和平面所成角的定义：

　　平面的一条斜线和它在平面内的射影所成的锐角，叫做这条直线和这个平面所成的角．

　　特别地：如果一条直线垂直于平面，我们说它们所成的角为直角，如果一条直线和平面平行或在平面内，我们说它们所成的角为0°,直线与平面所成角的范围为[0,].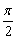

　　（2）求直线和平面所成角的步骤：

　　①作图——找出或作出直线与平面所成的角；

　　②证明——证明所找或所作的角即为所求角；

　　③计算——通常在三角形中计算．

　　（3）最小角定理：斜线和平面所成的角，是斜线和平面内经过斜足的一切直线所成角中的最小的角．

例2、如图，AO是平面M的斜线，O是斜足，AB⊥M于B，OD是M内不与OB重合的直线，∠AOB=α，∠BOD=β，∠AOD=γ.

　　求证：cosγ= cosα·cosβ.

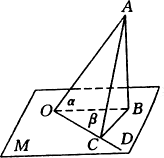
[证明]

例3、如图，在正方体ABCD—A1B1C1D1中，求：

（1）BC1与平面ABCD所成的角.

（2）BD1与平面A1B1C1D1所成的角.

（3）BC1与平面BDD1B1所成的角.

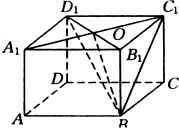
[解答]

3、三垂线定理

　　（1）三垂线定理：在平面内的一条直线，如果和这个平面的一条斜线的射影垂直，那么它也和这条斜线垂直．

　　

　　三垂线定理的逆定理：在平面内的一条直线，如果和这个平面的一条斜线垂直，那么它也和这条斜线的射影垂直．

　　（2）三垂线定理及其逆定理涉及了“四线一面”，四线即为斜线、垂线、射影及面内直线．

　　（3）三垂线定理及其逆定理涉及了“三个垂直”即：垂线与平面垂直；射影与平面内直线垂直；斜线与平面内直线垂直．

　　（4）三垂线定理是线线垂直的判定定理，这两条直线可以是相交直线，也可以是异面直线．

　　三垂线定理的逆定理也是线线垂直的判定定理，主要用来证共面直线垂直．

例4、如图，长方体ABCD—A1B1C1D1中，P、Q、R分别为棱AA1，BB1，BC上的点，PQ∥AB，∠D1QR=90°，求证：C1Q⊥PR.

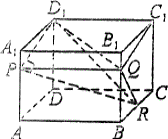
[证明]

例5、如图，△ABC所在平面α外一点P，已知PA⊥BC，PB⊥AC，求证：（1）P在平面α的射影是△ABC的垂心；（2）PC⊥AB．

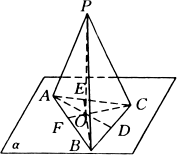
[证明]

例6、如图，平面α内有Rt△ABC，∠C=90°，P是平面α外一点且PA=PB=PC，P点到平面α的距离是40cm，AC=18 cm，求点P到BC的距离．

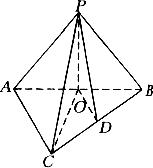
[解答]