|
一、一周知识概述
本周学习了一种新的运算——对数运算,它与加、减、乘、除、幂运算一样,具有自己的运算法则,由于对数是高中一重要内容,且是一个难点内容,我们要熟悉对数式与指数式的互化,熟练掌握其运算法则。对数的概念是我们进一步学习对数函数的基础,对数是由指数定义的,即对数的运算是指数运算的逆运算.因此,在研究指数与对数的有关问题时,要注意两者之间的等价转化.
对数的运算性质,对数恒等式、换底公式是进行对数式的化简、计算的基础,掌握好这些性质并能灵活运用,有利于提高我们的数学能力.
通过对对数概念的学习,培养学生分类讨论的能力、等价转化的能力以及运用所学知识分析问题,解决问题的能力.
二、重点知识归纳及讲解
1、对数的概念
一般地,如果a(a>0且a≠1)的b次幂等于N,即ab=N,那么数b就叫做以a为底N的对数,记作logaN=b,其中a叫做对数的底数,N叫做真数.
即 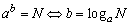 (a>0,a≠1,N>0) (a>0,a≠1,N>0)
说明:对数记号logaN只有在a>0且a≠1,N>0时才有意义.因为①若a<0且N为某些数值时,b不存在,如(-2)x=3.②若a=0,只有当N=0时logaN才存在.③若a=1,有时b不存在,如log12.
2、对数恒等式
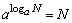 (a>0,a≠1,N>0) (a>0,a≠1,N>0)
3、对数的运算性质
设a>0,a≠1,M>0,N>0,则:
(1)loga(MN)=logaM+logaN;
(2)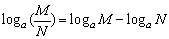 ; ;
(3)logaMn=nlogaM.
4、对数的换底公式
设a>0,a≠1,c>0,c≠1,N>0,则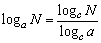 . .
三、难点知识剖析
1、对对数概念的理解:对数是定义在指数的基础之上的,就是说如果ab=N(a>0,a≠1),那么b=logaN,即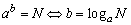 .由此,可以将对数问题转化为指数问题,也可以将指数问题转化为对数问题. .由此,可以将对数问题转化为指数问题,也可以将指数问题转化为对数问题.
常用对数是以10为底的对数.常用对数在数学中的作用就是解决计算问题.随着科学技术的发展,繁琐的计算已由计算机来承担,利用对数来解决计算已退出历史舞台,但对数的概念在数学中,仍然占有重要的地位.
自然对数是以e为底的对数,其中e=2.71828…为常数.
2、对数的运算性质是对数式化简、计算的基础,运用对数的运算性质可以把积、商的对数转化为对数的和、差,把幂的对数转化为幂指数与对数的积.同时还应注意公式的逆用.
3、对数的换底公式是进行对数式的化简,计算的重要工具,运用它可以将不同底的对数问题转化成同底的对数问题,结合对数的运算性质,即可使运算得以简化.
四、例题讲解
例1、(1)已知log427=a,log52=b,用a、b表示lg2、lg3.
(2)已知log67=a,3b=4,用a、b表示log127.
[解析]
例2、(1)计算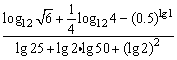 . .
(2)计算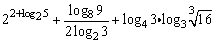 . .
[解析]
例3、设lga+lgb=2lg(a-2b),求log2a-log2b的值.
[解析]
例4、设x、y均为正数,且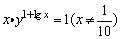 ,求lg(xy)的取值范围. ,求lg(xy)的取值范围.
[解析]
|