一、一周知识概述

　　本周学习对数函数的概念，图象、性质，对数函数是高中数学函数的重要内容．要求掌握对数函数的概念、图象及性质，并能运用对数函数的性质解决一些简单的应用问题．

　　对数函数是指数函数的反函数，因此学习对数函数的相关知识时，可结合指数函数的有关知识以及反函数的概念及性质，对指数函数及对数函数的相关知识进行比较，以加深对这两个函数的概念，图象及性质的理解．

　　通过对对数函数内容的学习，注意培养数形结合的能力，分类讨论的能力，等价转化的能力，以及运用所学知识分析问题，解决问题的能力．

二、重点知识归纳及讲解

1、对数函数的概念

函数y=logax（a＞0且a≠1）叫做对数函数.

2、对数函数的图象及性质.

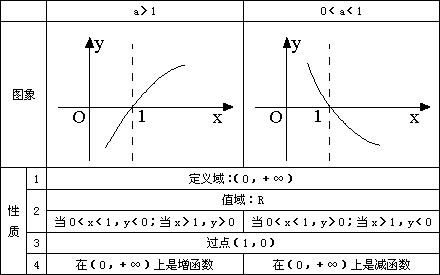
图象位置与底的大小的关系

 

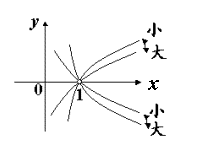
3、运用对数函数的性质，可以进行大小比较，解方程与不等式，求函数的最大值与最小值等．

三、难点知识剖析

1、函数y=logaf(x)的定义域等价于f(x)＞0的解集，而函数y=logaf(x)的值域，则应考虑x在定义域中取值时，f(x)的值域，再根据y=logax的单调性确定．

2、函数y=logaf(x)的单调性，一般先考虑使f(x)＞0的x的集合（即定义域），在定义域内f(x)的单调区间，再根据复合函数的单调性来确定.

3、形如logaf(x)= logag(x)的对数方程

方程

4、形如logaf(x)＞logag(x)的不等式

当a＞1时，不等式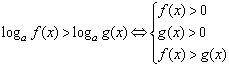

当0＜a＜1时，不等式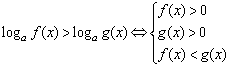

四、例题讲解

例1、求下列函数的值域和单调区间.

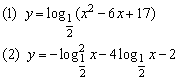
[解析]

例2、已知函数f(x)=lg(ax2＋2x＋1)（a∈R）.

（1）若函数f(x)的定义域为R，求实数a的取值范围；

（2）若函数f(x)的值域为R，求实数a的取值范围.

[解析]

例3、已知的最大值和最小值以及相应的x值.

[解析]

例4、已知f(x)=loga(ax－1)（a＞0，a≠1）.

（1）求f(x)的定义域；

（2）讨论f(x)的单调性；

（3）求函数y=f(2x)与y=f－1(x)的图象交点的横坐标.

[解析]

例5、在函数y=-logax(0<a<1，x≥1)的图像上有A、B、C三点，它们的横坐标分别为t，t＋2，t＋4．

(1)若△ABC的面积为S，求S=f(t)；

(2)判定S=f(t)的单调性并求其最大值．

[解析]