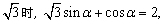4、根据函数图像提供的信息,求y=Asin(ωx+φ)+k的表达式.
若已知函数的图像求它对应的解析式,一般是仔细观察图像,从它提示出特征,如一个或半个周期,最高点与最低点,与x轴与y轴的交点或其他特殊点等.
如果所求函数解析式为y=Asin(ωx+φ),此时最大值与最小值互为相反数.A由图像的最高点与最低点确定,ω由周期T确定,T由相邻的两个最高点或最低点确定,φ由已知点的坐标确定.
如果函数的最大值与最小值不互为相反数,说明解析式为y=Asin(ωx+φ)+k的形式,设最大值为m,最小值为n,则A+k=m,-A+k=n,从而 .
.
值得注意的是,在将已知点的坐标代入解析式求φ的值时,φ可以有多个不同的点,因此由图像求得的y=Asin(ωx+φ)表达式不惟一.如果对φ的取值范围加以限制,则表达式是惟一确定的.
小结:
利用图像特征确定函数解析式y=Asin(ωx+φ)+k或根据代数条件确定解析式时,要注意以下几种常用方法:
(1)振幅 .
.
(2)相邻两个最值对应的横坐标之差,或者一个单调区间的长度为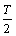 ,由此推出ω值.
,由此推出ω值.
(3)确定ω值,一般用给定特殊点坐标代入解析式来确定.
例2、单摆从某点开始来回摆动,离开平衡位置的距离S(厘米)和时间t(秒)的函数关系为:
(1)作出它的图像;
(2)单摆开始摆动(t=0)时,离开平衡位置多少厘米?
(3)单摆摆动到最右边时,离开平衡位置多少厘米?
(4)单摆来回摆动一次需多少时间?
解:(l)找出曲线上的五个特殊点,列表如下:
(2)当t=0时,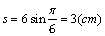 ,即单摆开始摆动时,离开平衡位置3cm.
,即单摆开始摆动时,离开平衡位置3cm.
(3) 的振幅为6,所以单摆摆动到最右边时,离开平衡位置6cm.
的振幅为6,所以单摆摆动到最右边时,离开平衡位置6cm.
(4) 的周期
的周期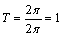 ,所以单摆来回摆动一次需要的时间为1s.
,所以单摆来回摆动一次需要的时间为1s.
评注:在作图时,如无特殊声明,一般用五点法作图较简便.
例3、函数f(x)的横坐标伸长到原来的两倍,再向左平移 个单位,所得到的曲线是
个单位,所得到的曲线是 的图像,试求函数y=f(x)的解析式.
的图像,试求函数y=f(x)的解析式.
分析:
这个问题有两种解法,一是考虑以上变换的“逆变换”,即将以上变换倒过来,由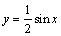 变换到y=f(x);二是代换法,即设y=Asin(ωx+φ),然后按题设中的变换分两步得:
变换到y=f(x);二是代换法,即设y=Asin(ωx+φ),然后按题设中的变换分两步得: ,它就是
,它就是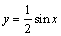 ,即可求得A、ω、φ的值.
,即可求得A、ω、φ的值.
解:解法一:
问题即是将 的图像先向右平移
的图像先向右平移 个单位,得到
个单位,得到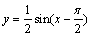 ;
;
再将横坐标压缩到原来的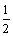 ,得
,得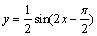 ,
,
即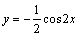 ,这就是所求函数f(x)的解析式、
,这就是所求函数f(x)的解析式、
解法二:
设y=Asin(ωx+φ),将它的横坐标伸长到原来的两倍得到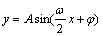 ;
;
再将其图像向左平移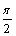 个单位,
个单位,
得 =
=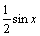 .
.
∴ 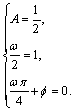 解之得:
解之得: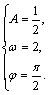
∴ 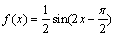 ,即
,即 .
.
小结:以上两种解法各有“千秋”,均为求解类似问题的好方法,注意熟练掌握.
例4、已知函数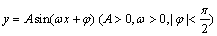 的图像的一个最高点为(2,
的图像的一个最高点为(2,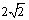 ),由这个最高点到相邻最低点,图像与x轴交于(6,0)点,试求这个函数的解析式.
),由这个最高点到相邻最低点,图像与x轴交于(6,0)点,试求这个函数的解析式.
解:
∵ 最高点为(2,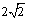 ),A=
),A=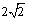 ,
,
由题意知从最高点到相邻最低点时交x轴于(6,0),
∴  ,即T=16.
,即T=16.
∴ 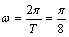 .
.
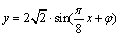 代入最高点坐标,
代入最高点坐标,
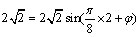 ,
,
∴  ,
, .
.
函数解析式为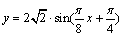 .
.
例5、函数y=Asin(ωx+φ)(A﹥0, ω﹥0)
(1)φ取何值时,f(x)为奇函数;
(2)φ取何值时,f(x)为偶函数.
分析:
判断函数的奇偶性首先要看定义域是否关于原点对称,然后判断f(-x)与f(x)的关系.
解答:
(1)∵x∈R,∴要使f(x)是奇函数,即f(x)+f(-x)=0,
即Asin(ωx+φ)+Asin(-ωx+φ)=0
∴2Asinφ·cosωx=0
∵cosωx不恒为0,
∴sinφ=0,即φ=kπ.
故φ=kπ时,f(x)为奇函数.
(2)若f(x)是偶函数,则 f(x)-f(-x)=0,即
Asin(ωx+φ)-Asin(-ωx+φ)=0
∴2Acosφ·sinωx=0
∵sinωx不恒为0,
∴cosφ=0,即φ= .
.
故φ=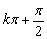 (k∈Z)时,f(x)为偶函数.
(k∈Z)时,f(x)为偶函数.
总结:由此题可类比得出函数y=Acos(ωx+φ)的奇偶性规律:
φ=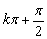 时,y=Acos(ωx+φ)是奇函数.
时,y=Acos(ωx+φ)是奇函数.
φ=kπ(k∈Z)时,y=Acos(ωx+φ)是偶函数.
例6、若f(x)=1-2a-2acosx-2sin2x的最小值为g(a).
(1)试用a表示出g(a);
(2)求使 的a的值,并对此a求f(x)的最大值.
的a的值,并对此a求f(x)的最大值.
分析:
本题可转化为二次函数在闭区间上的最值问题,需要根据对称轴与区间的位置关系进行分类讨论.
解答:(1)f(x)=1-2a-2acosx-2(1-cos2x)
=2cos2x-2acosx-2a-1
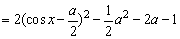
令cosx=t,t∈[-1,1],则
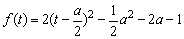
①当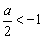 ,即a﹤-2时
,即a﹤-2时
由t=-1得,g(a)=1-2a+2a=1
②当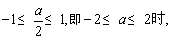

③当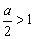 时,a﹥2时,由t=1得,g(a)=1-4a.
时,a﹥2时,由t=1得,g(a)=1-4a.
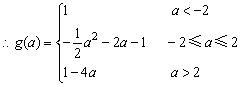
(2)要使g(a)=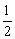 ,则a应在[-2,2]内,
,则a应在[-2,2]内,
由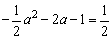 ,得a=-1或a=-3
,得a=-1或a=-3
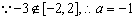
a=-1时,f(x)=2cos2x+2cosx+1=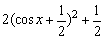
当cosx=1,即x=2kπ(k∈Z)时,f(x)的最大值为5.
例7、如图,已知水渠的横断面是等腰梯形,水渠的深度为h,横截面的面积为S,试求当水渠的倾斜角α为何值时,才能使水渗漏量最小,同时也能使水流的阻力最小?
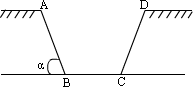
分析:
根据题意,要使水渠的水渗漏量及水流的阻力最小,即使(AB+CD+BC)的周长最小,因此本题可转化为三角函数的最值问题.
解答:
由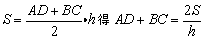
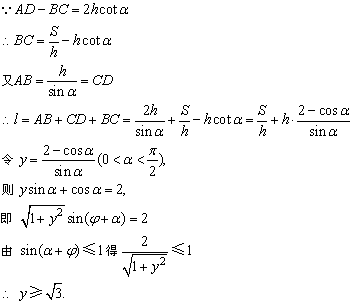
当y取最小值