|
一、一周知识概述
函数的单调性是函数的重要性质之一,它是研究函数值随自变量变化的一种趋势,如果函数值的变化与自变量的变化保持一致,则为增函数;如果函数值的变化与自变量的变化相反,则为减函数.
函数的单调性可以借助函数的图象来研究.具有单调性的函数的图象特征:增函数的图象是上升曲线,减函数的图象是下降曲线.
特别值得注意的是,函数的单调性与对应区间有关.
了解反函数的的概念及互为反函数的函数图象间的关系,掌握并会灵活应用互为反函数的函数图象间的关系.
二、知识要点归纳
1、函数的单调性
(1)设函数y=f(x)的定义域是M,区间D是M的一个子集,若对于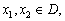 当x1<x2时,恒有f(x1)<f(x2)成立,则称函数y=f(x)在区间D上是单调递增函数. 当x1<x2时,恒有f(x1)<f(x2)成立,则称函数y=f(x)在区间D上是单调递增函数.
(2)设函数y=f(x)的定义域是M,区间D是M的一个子集,若对于 当x1<x2时,恒有f(x1)>f(x2)成立,则称函数y=f(x)在区间D上是单调递减函数. 当x1<x2时,恒有f(x1)>f(x2)成立,则称函数y=f(x)在区间D上是单调递减函数.
(3)单调函数:
单调递增函数与单调递减函数统称为单调函数.若y=f(x)在区间D上为单调函数,则称D是这个函数的单调区间.
2、单调函数的基本性质
(1)y=f(x)在区间I上是单调递增(减)函数,c,d都是常数,则y=cf(x)+d在I上也是单调函数.若c>0,y=cf(x)+d在I上是单调递增(减)函数;若c<0,y=cf(x)+d在I是单调递减(增)函数.
(2)若函数y=f(x)与y=g(x)在区间I上同为单调递增(减)函数,则y=f(x)+g(x)在I上也是单调递增(减)函数.
(3)u=g(x)在区间(a,b)上为增(减)函数,y=f(u)在(g(a),g(b))(或(g(b), g(a)))上为增(减)函数,则y=f(g(x))在(a,b)上为增函数.
(4)u=g(x)在(a,b)上为增(减)函数,y=f(u)在(g(a),g(b))(或(g(b),g(a)))上为减(增)函数,则y=f(g(x))在(a,b)上为减函数.
3、一次函数,反比例函数和二次函数的单调性
函数 |
y=ax+b
(a≠0)
|
y=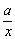 (a≠0) (a≠0) |
y=ax2+bx+c(a≠0) |
单调
区间
|
(-∞,+∞)
|
(-∞,0) |
(0,+∞) |
(-∞,- ] ] |
[- ,+∞) ,+∞) |
单
调
性
|
a>0 |
增函数 |
减函数 |
减函数 |
减函数 |
增函数 |
a<0 |
减函数 |
增函数 |
增函数 |
增函数 |
减函数 |
4、反函数的概念:
(1)只有自变量x与其对应的函数值y是一一对应的函数才存在反函数,反函数的对应法则是原函数对应法则f的逆对应,反函数的定义域、值域分别是原函数的值域、定义域.
(2)互为反函数的两个函数的图象关于直线y=x对称,即点(a,b)在y=f(x)的图象上,则点(b,a)必在y=f-1(x)图象上.
(3)互为反函数的两个函数具有相同的单调性.
5、反函数的性质
(1)y =f-1(x)是y=f(x)的反函数,则y=f(x)也是y =f-1(x)的反函数,即y=f(x)和y
=f-1(x)互为反函数.
(2)函数y=f(x)存在反函数的充要条件是函数y=f(x)是定义域到值域的一一映射.
(3)函数y=f(x)和反函数y =f-1(x)的定义域,值域互换,即
| |
函数y=f(x) |
函数y =f-1(x) |
定义域 |
A |
C |
值域 |
C |
A |
6、互为反函数的图象关系
函数y=f(x)的图象和它的反函数y =f-1(x)的图象关于直线y=x对称.
7、反函数与原函数的其它性质和联系
(1)反函数与原函数
f[f-1(x)]=x,f-1[f(x)]=x
注:f-1 [f-1(x)])并不是反函数的反函数,而是y=f-1(x)与自身形成的复合函数,谨防出现f-1 [f-1(x)]=f(x)的错误作法.
(2)反函数与单调性
如果函数y=f(x)有单调性,则反函数y=f-1(x)也有与y=f(x)一致的单调性,即y=f(x)在[a,b]上为增函数,则y=f-1(x)在[f(a),f(b)]上为增函数;y=f(x)在[a,b]上为减函数,则y=f-1(x)在[f(b),f(a)]上为减函数.
8、复合函数的单调性
复合函数y=f[g(x)]的单调性规律是“同则增,异则减”,即f(u)与g(x)若具有相同的单调性,则f[g(x)]必定是增函数,若具有不同的单调性,则f[g(x)]必定是减函数,讨论复合函数单调性的步骤是:
(1)求出复合函数的定义域;
(2)把复合函数分解成若干个常见的基本函数,并判定其定义域;
(3)把中间变量的变化范围转化为自变量的变化范围;
(4)根据上述复合函数的单调性规律判定其单调性.
三、方法指导
1、判定函数单调性的方法
(1)定义法:根据函数单调性的定义进行证明,其步骤如下:
第一步:取值.即设x1、x2是该区间内的任意两个值,且x1<x2.
第二步:作差变形.即作差f(x1)-f(x2),并通过因式分解,配方,有理化等方法,向有利于判断差的符号的方向变形.
第三步:定正负.确定差f(x1)-f(x2)的正负,当正负不确定时,可以进行分区间讨论.
第四步:判断.根据定义作出结论.
即“取值——作差变形——定正负——判断”这几个步骤.
(2)直接法:运用已知的结论,直接得到函数的单调性.如一次函数,
二次函数,反比例函数的单调性均可直接说出,注意了解以下一
些结论,对于直接判断函数的单调性有好处:
①函数y=-f(x)与函数y=f(x)的单调性相反.
②当f(x)恒为正或恒为负时 ,函数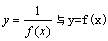 的单调性相反. 的单调性相反.
③在公共区间内,增函数+增函数=增函数,增函数-减函数=增函数等.
(3)图象法:根据函数的图象进行判断.
四、重点知识评析
1、如何判定函数的单调性?
例1、讨论函数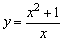 (x>0)的单调性. (x>0)的单调性.
[解析]
2、如何求复合函数的单调区间?
例2 已知f(x)=8+2x-x2, g(x)=f(2-x2),试求g(x)的单调区间.
[解析]
3、如何求反函数?
例3、已知函数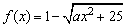 (-5≤x≤0),点P(-2,-4)在它的反函数的图象上. (-5≤x≤0),点P(-2,-4)在它的反函数的图象上.
(1)求f(x)的反函数f-1(x);
(2)证明f-1(x)在其定义域上是减函数.
[解析]
4、如何利用反函数求值域?
例4、求函数的值域

[解析]
5、如何利用互为反函数图象的对称性解决问题?
例5、已知函数y=kx+b的图象过(1,2)点,它的反函数f-1(x)的图象过(4,0)点,
求函数f(x)的解析式.
[解析]
例6、设f(x)的定义域为(0,+∞),且对一切x、y>0,都有 =f(x)-f(y),当x>1时,有f(x)>0. =f(x)-f(y),当x>1时,有f(x)>0.
(1)求f(1)的值;
(2)判断f(x)的单调性并证明;
(3)若f(6)=1,解不等式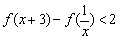 . .
[解析]
|