本周学习函数的概念、映射的概念及函数的表示法，函数解析式、定义域、值域的求法。
函数的定义及其有关概念是本章的核心内容，函数思想是贯穿整个中学代数方面的核心思想。
高中函数概念是建立在集合论的基础之上的.用集合的观点来定义函数更能体现函数的本质.通过对函数概念及函数表示法的学习，培养学生分析问题，解决问题的能力，初步的数学建模能力，数形结合的能力和化归的思想及转化的能力.
1、映射的概念
（1）映射是特殊的对应，即是“一对一”的对应和“多对一”的对应，而“一对多”的对应不是映射.
（2）给定一个映射f：A→B，则A中的每一个元素都有唯一的象，B的某些元素可以没有原象，如果有原象，也可以不唯一的.
2、函数的概念
（1）函数是特殊的映射，即集合A、B均为非空数集的映射.
（2）构成函数的三要素；对应关系f、定义域A、值域{f(x)|x∈A}，其中值域
{f(x)|x∈A}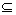
B.
正确理解函数符号y=f(x)：
①它表示y是x的函数，绝非f与x的积；
②f(a)仅表示函数f(x)在x=a时的函数值，是一常数．
（3）确定函数的条件.
当对应关系f和定义域A已确定，则函数已确定，判定两个函数是否相同时，就要看定义域和对应法则是否完全一致．
（4）函数的定义域，一般是使函数解析式有意义的x值的集合，在具体问题中则应考虑x的实际意义，如时间t，距离d均应为非负数等.
求函数定义域的基本方法：
①分式中分母不为零；
②偶次根式中的被开方式不小于零；
③ [f(x)]0中的底f(x)不为零；
④如果f(x)是由几个部分的数学式子构成的，那么函数的定义域是使每个部分式子都有意义的实数集合．
根据对应法则的性质求定义域，如已知f(x)的定义域为[a，b]，则f[ψ（x）]的定义域应为ψ（x）的定义域与a≤ψ（x）≤b的解集的交集．
3、函数的表示法
解析法、列表法、图象法.
我们所研究的函数大多都是用解析法表示的函数，其特点是函数关系清楚.但要明确解析法并不是表示函数的唯一方法，还可以用列表法，图象法来表示，且并不是任何函数都可以用解析法表示，对定义域是有限数集的函数，列表法就显示了它的优点.
4、函数的值域是全体函数值所组成的集合，有观察法，换元法、配方法、图象法、反求法、判别式法等求值域的基本方法．
函数的值域是函数的“三要素”之一，在一个给定的函数中，函数的值域随对应法则和定义域而确定．
几个基本初等函数的值域：
一次函数y=kx＋b（k≠0）的值域：{y|y∈R}；
二次函数y=ax2＋bx＋c（a≠0）的值域：
当a>0时，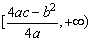
；
当a<0时，
；
反比例函数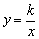
（k≠0）的值域：（－∞，0）∪（0，＋∞）．
求函数值域的基本方法
（1）直接法：从自变量x的范围出发，推出y=f(x)的取值范围；
例如：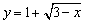
的值域为[1，＋∞）．
这是因为x≤3，所以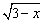
≥0，∴
y≥1.
（2）二次函数法：利用换元法将函数转化为二次函数求值域（或最值）；
（3）反函数法：将求函数值域转化为求反函数的定义域；
（4）判别式法：运用方程的思想，将函数变形成关于x的二次方程，依据二次方程有实根，求出y的取值范围；
（5）利用函数的单调性求值域；
（6）图象法：作出函数的图象，由图象来确定函数的值域．
1、求函数定义域
求由几个代数式的和构成的函数解析式的函数的定义域，应先求出各个代数式有意义的自变量x的集合，再求出这些集合的交集.即设函数f(x)=f1(x)＋f2(x)＋…＋fn(x)的定义域为A，fi(x)(i=1,2,…,n)的定义域为Ai，则A=A1∩A2∩…∩An，求解常常是通过解不等式组来解决.
2、求函数解析式
在某些问题中，给出了自变量x与函数y的函数关系，要求函数解析式，一般要根据题设条件分析函数y与自变量x之间的数量关系.应注意有时自变量在不同的范围取值时，x与y之间的数量关系不一样，这时需要多个解析式来表示这个函数（即分段函数）.
的定义域.
)的值.