|
一、一周知识概述
本周学习内容为1.6逻辑联结词、 1.7四种命题及1.8充分条件与必要条件.理解逻辑联结词“或”、“且”、“非”的含义,理解并掌握四种命题及其相互关系,掌握充分条件与必要条件,关键是要掌握关于充要条件的判断.掌握反证法。
二、重难点知识的归纳与剖析
1.“或”、“且”、“非”这些词叫做逻辑联结词.不含逻辑联结词,是简单命题;由简单命题与逻辑联结词构成,是复合命题.或、且、非是三种最基本的逻辑联结词.课本给出了三种简单的复合命题“p且q”,“p或q”和“非p”的真值表:

2.四种命题的形式是:
原命题:若p则q,
逆命题:若q则p
否命题:若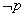 则 则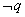 , ,
逆否命题:若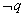 则 则 . .
四种命题之间的相互关系
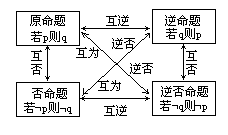
3.一个命题的真假与其它三个命题的真假有如下三条关系:
(1)原命题为真,它的逆命题不一定为真.
例如,原命题“若a=0,则ab=0”是真命题,它的逆命题“若ab=0,则a=0”是假命题.
(2)原命题为真,它的否命题不一定为真.
例如,原命题“若a=0,则ab=0”是真命题,它的否命题“若a≠0,则ab≠0”是假命题.
(3)原命题为真,它的逆否命题一定为真.
例如,原命题“若a=0,则ab=0”是真命题,它的逆否命题“若ab≠0,则a≠0”是真命题.
4.从逻辑推理关系上看
(1)若p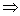 q且q q且q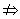 p,则p是q的充分而不必要条件; p,则p是q的充分而不必要条件;
(2)若q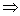 p且p p且p q,则p是q的必要而不充分条件; q,则p是q的必要而不充分条件;
(3)若p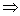 q且q q且q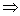 p(或p p(或p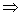 q且 q且 p p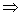  q)则p是q的充要条件; q)则p是q的充要条件;
(4)若p q且q q且q p,则p既不是q的充分条件也不是q的必要条件。 p,则p既不是q的充分条件也不是q的必要条件。
从集合与集合之间关系上看
(1)若A B,则A是B的充分条件; B,则A是B的充分条件;
(2)若A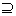 B,则A是B的必要条件; B,则A是B的必要条件;
(3)A=B,则A是B的充要条件;
(4)若A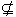 B且B B且B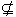 A,则A既不是B的充分条件,也不是B的必要条件。 A,则A既不是B的充分条件,也不是B的必要条件。
三、难点知识剖析
1.对反证法的理解
①反证法的理论根据是:原命题为真,则它的逆否命题也为真.在直接证明原命题有困难时,就可转化为证明它的逆否命题成立.
②用反证法证明命题的一般步骤是
第一步:假设命题的结论不成立,即假设结论的反面成立;
第二步:从这个假设出发,经过推理论证,得出矛盾;
第三步:由矛盾判定假设不正确,从而肯定命题的结论正确.
③一般地来说,在什么条件下(或问题中)想到用反证法来证明,下面提供几种情形作为参考.
第一,问题共计有n种情况,现要证明其中一种情况成立时,可想到用反证法证明把其他的 n-1种情况都排除,从而确定这种情况成立.
如要证明两条直线相交,可用反证法证明这两条直线平行不成立,因为在同一平面内,两条直线的位置关系是平行或相交,平行不成立,那么间接的证明两条直线相交;
第二,命题用否定形式叙述的,如证明2不是方程2x+1=0的根,可用反证法证明,假设2是方程2x+1=0的根,则2×2+1应等于0,而2×2+1=5,产生矛盾,从而确定2不是方程2x+1=0的根成立;
第三,命题用“至少”的字样叙述时,可用反证法证明,如证明a≠b,b≠c至少有一个成立,那我们可用反证法证明如下:假设a≠b,b≠c都不成立,即a=b且b=c,从这一条件出发推得矛盾,故a=b,且b=c不成立,因此,a≠b,b≠c至少有一个成立;
第四,当命题成立非常明显,而要直接证明,所用的理论不少,且不容易说明白,而它的逆命题易证,如(1)中的举例,证明两条直线相交的依据几乎没有,而平行线有很多性质,易于推理,因此,用反证法把证明两条直线相交问题转化到平行线的性质.
2.否命题与命题的否定是两个不同的概念
若p表示命题,“非p”叫做命题的否定.如果原命题是“若p则q”,那么这个原命题的否定是“p则非q”,即只否定结论.
原命题的否定命题是“若非p,则非q”,即否定条件又否定结论,例如“菱形的四条边都相等”的否定为“菱形的四条边不都相等”;把“菱形的四条边都相等”作为原命题,则它的否命题是“若四边形不是菱形,则它的四条边不都相等.”
3.三个逻辑联结词与集合的交、并、补运算的关系。
(1) 对“或”的理解可联想到集合中“并集”的概念, 或 或 中的“或”,它是指“x∈A”或“x∈B”中至少有一个是成立。 中的“或”,它是指“x∈A”或“x∈B”中至少有一个是成立。
(2) 对“且”的理解,可联想到集合中“交集”的概念,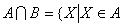 或 或 中的“且”
是指“x∈A”或“x∈B”这两个条件都要满足。 中的“且”
是指“x∈A”或“x∈B”这两个条件都要满足。
(3) 对“非”的理解,可联想到集合中的“补集”概念,若命题中对应于集合P,则命题非P就应对应着集合P在全集U中的补集CuP。
4.用集合观点来理解“充分条件”、“必要条件”、“充要条件”
(1) 若p q,则p是q的充分条件;若p q,则p是q的充分条件;若p q,则p是q的必要条件。设A={x|p},B={x|q},如果A q,则p是q的必要条件。设A={x|p},B={x|q},如果A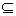 B,就是x∈A则x∈B,则A是B的充分条件,即p B,就是x∈A则x∈B,则A是B的充分条件,即p q。如图: q。如图:

(2) 若A=B则A是B的充要条件,即p q. q.
5.结合转化思想、数形结合思想等用集合观点来解决《简易逻辑》中一些问题。
例1、写出若a、b<0则a<0且a>0的否命题
分析:
“若p则q”的否命题“若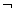 p则 p则 q”,它涉及了逻辑联结词的否定,对此我们从集合角度来看,a<0且b>0可表示为一个点集A,用图形表示。如图,不满足“a<0且b>0”的点(a,b),在阴影的另一部分,即 q”,它涉及了逻辑联结词的否定,对此我们从集合角度来看,a<0且b>0可表示为一个点集A,用图形表示。如图,不满足“a<0且b>0”的点(a,b),在阴影的另一部分,即 。它可以看作是X轴及以下部分(b≤0)和Y轴及右侧部分(a≥0)部分合起来构成,即两块区域的并集,
a、b满足“a≥0或b≤0”。 。它可以看作是X轴及以下部分(b≤0)和Y轴及右侧部分(a≥0)部分合起来构成,即两块区域的并集,
a、b满足“a≥0或b≤0”。
因而,否命题为若a、b≥0则a≥0或b≤0。

说明:“p且q”的否定为“非p或非q”,用集合的观点来解释,并结合图形,同学更容易接受并理解。
例2、对实数x、y、“|x|+|y|≤1”是“|x|≤1,|y|≤1”的什么条件?
分析:
从集合的角度判断,考虑集合A={(x,y)|
|x|+|y|≤1}与B={(x,y)| |x|≤1,|y|≤1}的包含关系。如图
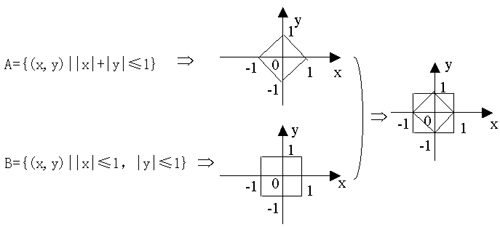
可以知道,A B,所以
|x|+|y|≤1是|x|≤1,|y|≤1的充分而不必要条件。 B,所以
|x|+|y|≤1是|x|≤1,|y|≤1的充分而不必要条件。
说明:充分条件、必要条件充要条件是重要的数学概念,在判断时应①确定条件是什么、结论是什么;②尝试从条件推导结论,从结论推导条件;③确定条件是结论的什么条件。而前面我们已经用集合的观点来概括“充分”、“必要”、“充要”条件,因此解决这类问题时,有时可以借助集合的运算及包含关系来解决。
四、例题讲解
例1、判断下列命题的真假,并写出它的逆命题,否命题,逆否命题,同时,也判断这些命题的真假.
①若a>b,则ac2>bc2
②若a>b,则 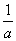 < <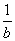
③若一个式子是等式,则它的两边都乘以同一个数,所得结果仍是等式
④若圆心到直线的距离等于半径,则该直线是圆的切线
⑤若四边形的对角互补,则该四边形是圆的内接四边形
⑥若在二次函数y=ax2+bx+c中,b2-4ac<0,则该二次函数图像与x轴有公共点
分析:
要判断命题的真假性,关键是看条件是否能推出结论,如果能,则是真命题,如果不能,则是假命题.写出其它的几个命题时,关键是分清条件和结论以及条件和结论的否定.
解:
① ∵当c=0时,ac2=bc2,∴该命题为假命题
逆命题:若ac2>bc2,则a>b.为真
否命题:若a≤b,则ac2≤bc2.为真
逆否命题:若ac2≤bc2,则a≤b.为假
② 该命题为假命题:∵ 当a>0,b<0时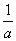 > >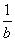 ; ;
逆命题:若 < < ,则a>b.为假(如b>0,a<0时) ,则a>b.为假(如b>0,a<0时)
否命题:若a≤b,则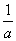 ≥ ≥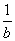 .为假(如b>0,a<0时) .为假(如b>0,a<0时)
逆否命题:若  ≥ ≥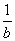 ,则a≤b.为假(如a>0,b<0时) ,则a≤b.为假(如a>0,b<0时)
③ 该命题为真,这是等式的性质
逆命题:若两个式子都乘以同一个数,所得结果相等,则这两个式子相等.为假,如把x和x2+1都乘以0后相等,但x≠x2+1
否命题:若两个式子不相等,则把它们都乘以同一个数,所得结果也不相等.为假
逆否命题:若两个式子都乘以同一个数,所得结果的不相等,则这个两式也不相等.为真
④ 该命题为真
逆命题:若直线是圆的切线,则圆心到直线的距离等于半径.为真
否命题:若圆心到直线的距离不等于半径,则该直线不是圆的切线.为真
逆否命题:若直线不是圆的切线,则圆心到直线的距离不等于半径.为真
⑤ 该命题为真
逆命题:若四边形是圆的内接四边形,则四边形的对角互补.为真
否命题:若四边形的对角不互补,则该四边形不是圆的内接四边形.为真
逆否命题:若四边形不是圆的内接四边形,则四边形的对角不互补.为真
⑥ 该命题为假,∵当b2-4ac<0时,二次方程ax2+bx+c=0没有实根.因此二次函数y=ax2+bx+c的图像与x轴无公共点.
逆命题:若二次函数y=ax2+bx+c的图像与x轴有公共点,则b2-4ac<0.为假
否命题:若二次函数y=ax2+bx+c中,b2-4ac≥0,则该二次函数图像与x轴没有公共点.为假
逆否命题:若二次函数y=ax2+bx+c的图像与x轴没有公共点,则b2-4ac≥0,为假.
点评:
1.写出一个命题的逆命题,否命题及逆命题的关键是分清原命题的条件和结论,然后按定义来写.
2.在判断原命题、逆命题、否命题、逆否命题的真假时,要利用原命题与其逆否命题的等价性(即同真同假),逆命题与否命题的等价性.
例2、设集合A、B是全集U的两个子集,则A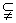 B是 B是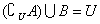 的( ) 的( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
解:
若A B,用文氏图可知 B,用文氏图可知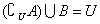 成立。若 成立。若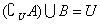 ,比如A=B满足条件,但A ,比如A=B满足条件,但A B不成立。所以A B不成立。所以A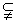 B是 B是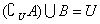 的充分不必要条件。 的充分不必要条件。
答案:A
例3、已知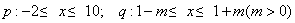 .若 .若 是 是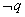 的必要而不充分条件,求实数m的取值范围. 的必要而不充分条件,求实数m的取值范围.
分析:可以有两个思路:
(1)先求出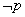 和 和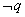 ,然后根据 ,然后根据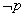 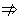  , , 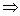 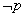 ,求得m的取值范围; ,求得m的取值范围;
(2)若原命题为“若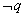 ,则 ,则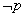 ”,其逆否命题是“若p则q”,由于它们是等价的,可以把求 ”,其逆否命题是“若p则q”,由于它们是等价的,可以把求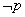 是 是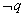 的必要而不充分条件等价转换为求p是q的充分而不必要条件. 的必要而不充分条件等价转换为求p是q的充分而不必要条件.
解法一 可求出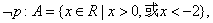
 . .
由 是 是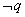 的必要而不充分条件,知 的必要而不充分条件,知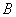 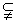 A,它等价于 A,它等价于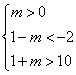
解得m的取值范围是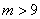 . .
解法二
根据思路二,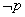 是 是 的必要而不充分条件,等价于p是q的充分而不必要条件.设 的必要而不充分条件,等价于p是q的充分而不必要条件.设
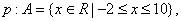
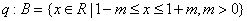 . .
所以,A B,它等价于 B,它等价于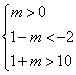
同样解得m的取值范围是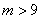 . .
例4、已知下列三个方程:
x2+4ax-4a+3=0,
x2+(a-1)x+a2=0,
x2+2ax-2a=0
至少有一个方程有实数根,求实数a的取值范围.
分析:
从正面入手,本题所要考虑的情况较多,但其反面情况仅有一种情况,故可考虑用反证法的思想去求解.
解答:假设三个方程均无实数根,则有
(4a)2-4×(-4a+3)<0, ①
(a-1)2-4a2<0, ②
(2a)2-4×(-2a)<0. ③
由①得4a2+4a-3<0,即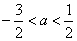
由②得(a+1)(3a-1)>0,即a<-1,或
由③得a(a+2)<0,即-2<a<0.
取①、②、③的并集得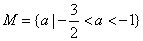
则使三个方程至少有一个方程有实根的实数a的取值范围应为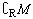 ,即 ,即
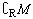 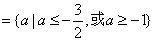
评析:
本题要求“三个方程中至少有一个方程有实数根时的a的取值范围”,只要求“其反面即三个方程均无实数根时a的取值集合M,再求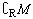 即可”.这种反证法的思想很重要,用起来也很简洁明了.否则,用直接法求a的取值范围将是很困难的. 即可”.这种反证法的思想很重要,用起来也很简洁明了.否则,用直接法求a的取值范围将是很困难的.
|