1.集合的有关概念
一组对象的全体形成一个集合,集合里的各个对象叫做集合的元素
⑴集合中的元素具有以下的特性
①确定性:任给一元素可确定其归属.即给定一个集合,任何一个对象是不是这个集合的元素也就确定了.
例如,给出集合{1,2,3,4},它只有1、2、3、4四个元素,其他对象都不是它的元素;
而“所有的好人”、“视力比较差的全体学生”、“我国的所有小河流”就不能视为集合,因为组成它们的对象是不能确定的.
② 互异性:集合中的任何两个元素都是不同的对象,也就是说,集合中的元素必须是互不相同的(即没有重复现象),相同的元素在集合中只能算作一个.例如,不能有{1,1,2},而必须写成{1,2}.
③ 无序性:集合中的元素间是无次序关系的.例如,{1,2,3}与{3,2,1}表示同一个集合.
(2)集合的元素
某些指定的对象集在一起就成为一个集合,集合中的每个对象叫做这个集合的元素.若a是集合A的元素,就说a属于集合A,记作a∈A.不含任何元素的集合叫做空集,记作Φ.
(3)集合的分类:有限集与无限集.
(4)集合的表示法:列举法、描述法和图示法.
列举法:将所给集合中的元素一一列举出来,写在大括号里,元素与元素之间用逗号分开,常用于表示有限集.
描述法:将所给集合中全部元素的共同特性和性质用文字或符号语言描述出来.常用于表示无限集.
使用描述法时,应注意六点:
①写清集合中元素的代号;
②说明该集合中元素的性质;
③不能出现未被说明的字母;
④多层描述时,应当准确使用“且”,“或”;
⑤所有描述的内容都要写在大括号内;
⑥用于描述的语句力求简明、确切.
图示法:画一条封闭的曲线,用它的内部来表示一个集合,常用于表示又需给具体元素的抽象集合,对已给出了具体元素的集合当然也可用图示法来表示.
如:A={1,2,3,4}
例1、设集合A={a,a+b, a+2b},B={a,ac,ac2},且A=B,求实数c值.
分析:
欲求c值,可列关于c的方程或方程组,根据两集合相等的意义及集合元素的互异性,有下面两种情况:(1)a+b=ac且a+2b= ac2,(2)a+b= ac2且a+2b=ac两种情况.
解析:
(1)a+b=ac且a+2b= ac2,消去b得:a+ ac2-2ac=0.∵a=0时,集B中三元素均为零,根据集合元素互异性舍去a=0.∴c2-2c+1=0,即c=1,但 c=1时,B中的三个元素也相同,舍去c=1,此时无解.
(2)a+b= ac2且a+2b=ac,消去b得: 2ac2-ac-a=0.∵a=0时,集B中三元素均为零,根据集合元素互异性舍去a=0.∴2c2-c-1=0,即c=1或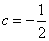 ,但 c=1时,B中的三个元素也相同,舍去c=1,∴
,但 c=1时,B中的三个元素也相同,舍去c=1,∴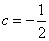 .
.
点评:
两集合相等的意义是两集合中的元素都相同,在求集合中元素字母的值时,可能产生与互异性相矛盾的增解,这需要解题后进行检验,去伪存真.
(5)常用数集及专用记号
①非负整数集(或自然数集)N={0,1,2,……}
②正整数集N*(或N+)={1,2,3,……}
③整数集Z={0,±1,±2,……}
④有理数集Q={整数与分数}
⑤实数集R={数轴上的点所对应的数}.
强调:实数集不可记为{R}或{实数集},0≠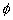 ≠{
≠{ } ,
} ,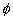 ≠{0},
≠{0},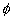 ≠{空集}.
≠{空集}.
1、要注意区分一些容易混淆的符号
(1) 与
与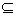 的区别:
的区别: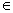 表示元素与集合之间的关系,例如1
表示元素与集合之间的关系,例如1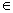 N,-1
N,-1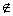 N等;
N等;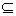 表示集合与集合之间的关系,例如N
表示集合与集合之间的关系,例如N R,
R,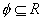 等.
等.
(2)a与{a}的区别:一般地,a表示一个元素,{a}而表示只有一个元素a的集合.例如,0 {0},{1}
{0},{1}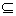 {1,2,3}等,不能写成0={0},{1}
{1,2,3}等,不能写成0={0},{1}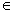 {1,2,3},1
{1,2,3},1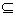 {1,2,3}.
{1,2,3}.
(3){0}与Φ的区别:{0}是含有一个元素0的集合,Φ是不含任何元素的集合,因此Φ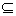 {0}但不能写成Φ={0},Φ
{0}但不能写成Φ={0},Φ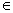 {0}.
{0}.
例3、已知集合M={x|x≤3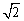 },集合P={x|x<2
},集合P={x|x<2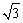 },设
},设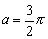 ,则下列关系式中正确的一个是( )
,则下列关系式中正确的一个是( )
A、P∈M B、a∈M
C、P M D、{a-3}
M D、{a-3}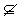 P
P
解析:
集合M、P都是部分实数组成的集合,而a是一个具体的实数,故M、P间的关系应用“包含”,“不包含”来确定,而对a与集合M、P的关系只能用“属于”,“不属于”来确定,比较实数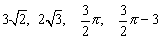 的大小,易判断C正确.
的大小,易判断C正确.
小结:正确使用集合的符号是正确分析、解答问题的关键.
2.理解集合所表示的意义
(1)对由条件给出的集合,要明白它所表示的意义,即元素指什么,是什么范围.如{y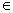 R|y=
R|y=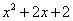 }表示的为函数y=
}表示的为函数y= 中y的取值范围,故{y
中y的取值范围,故{y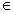 R|y=
R|y=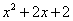 }={y
}={y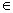 R|y
R|y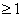 };而{x
};而{x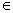 R|y=
R|y=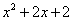 }表示y=
}表示y=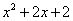 的x的取值范围,故{x
的x的取值范围,故{x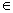 R|y=
R|y=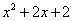 }=R.
}=R.
(2)用集合表示不等式(组)的解集时,要注意分辨是交集还是并集,结合数轴或韦恩图的直观性帮助思维判断.空集是任何集合的子集,但因为不好用韦恩图表示,容易被忽视,如在关系式B A中,易漏掉B=Φ的情况.
A中,易漏掉B=Φ的情况.
例4、 设A=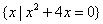 ,B=
,B=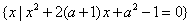
(1)若A B=B,求
B=B,求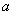 的值;
的值;
(2)若A B=B,求
B=B,求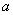 的值.
的值.
分析:
明确A B=B和A
B=B和A 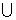 B=B的含义,根据问题的需要,将A
B=B的含义,根据问题的需要,将A B=B和A
B=B和A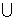 B=B转化为等价的关系式:
B=B转化为等价的关系式: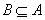 和
和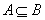 ,是解决本题的关键.
,是解决本题的关键.
解析:首先化简集合A,得A={-4,0}
(1)由于A  B=B,则有
B=B,则有 可知集合B或为空集Φ,或只含有根0或-4.
可知集合B或为空集Φ,或只含有根0或-4.
①若B=Φ,由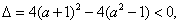 得
得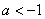
②若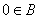 ,代入得:
,代入得: ,
,
当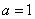 时,B=
时,B=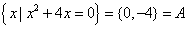 ,合题意.
,合题意.
当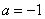 时,B=
时,B=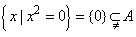 ,也符合题意.
,也符合题意.
③若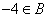 ,代入得:
,代入得: ,
,
当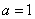 时,②中已讨论,合题意
时,②中已讨论,合题意
当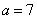 时,B=
时,B=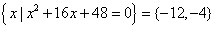 不合题意.
不合题意.
由①、②、③得,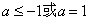 .
.
(2)因为A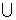 B=B,所以
B=B,所以 ,又A={-4,0},而B至多只有两个根,因此应有A=B.
,又A={-4,0},而B至多只有两个根,因此应有A=B.
由(1)知,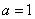
【点评】:
一般对于A B=B和A
B=B和A B=B这种类型的问题,都要注意转化为等价的关系式:
B=B这种类型的问题,都要注意转化为等价的关系式: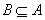 和
和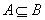 ,且在包含关系
,且在包含关系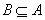 中,注意不要漏掉B=
中,注意不要漏掉B=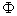 的情况.
的情况.
并且当A、B中的元素的个数相同时,还存在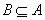 或
或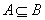 的情况时,只有A=B这一种情况.
的情况时,只有A=B这一种情况.