1、两角和与差的余弦公式
cos(α＋β)=cosαcosβ－sinαsinβ(C(α＋β))
cos(α－β)=cosαcosβ＋sinαsinβ(C(α－β))
[点拨]
（1）上述公式对α、β取任意角都成立.
（2）公式特点：公式中右边有两项，中间符号与左边角间符号相反，两项排列顺序是：cosαcosβ、sinαsinβ.
（3）牢记公式并能熟练进行左、右互化.
如化简：cos(α＋β)cosβ＋sin(α＋β)sinβ时，不要将cos(α＋β)、sin(α＋β)展开，而应就整个式子直接用公式化为cos[(α＋β)－β]=cosα.
（4）和（差）角公式可看成诱导公式的推广，诱导公式可看成和（差）角公式的特例.当α、β中有一个角为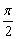
的整数倍时，以利用诱导公式较为简捷.
2、两角和与差的正弦公式
sin(α＋β)=sinαcosβ＋cosαsinβ(S(α＋β))
sin(α－β)=sinαcosβ－cosαsinβ(S(α－β))
[点拨]
（1）上述公式对α、β取任意角都成立.
（2）公式特点：右边有两项，中间的符号与左边角间符号一致，两项顺序为：sinαcosβ、cosαsinβ.
（3）牢记公式并能熟练进行左、右互化.如化简sin(α＋β)cosβ＋cos(α＋β)sinβ=?可直接用公式化简为sin[(α＋β)＋β]=sin(α＋2β).
（4）两角和与差的三角函数是诱导公式的推广，诱导公式是它的特例，当α、β中有一个角为90°的整数倍时，用诱导公式较为简便.
3、两角和与差的正切公式
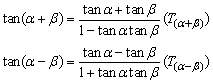
[点拨]
（1）Tα＋β中：α、β、α＋β都不取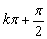
（k∈Z）时，公式才适用；Tα－β中：α、β、α－β都不取
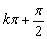（k∈Z）时，公式才适用.
（2）如α、β、α±β有一个角取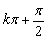
（k∈Z）时，可用诱导公式，
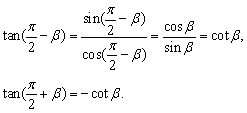
（3）公式特征：右边分子为两项：tanα、tanβ，中间符号与右边角间符号一致；右边分母为两项：1，tanαtanβ，中间符号与左边角间符号相反.
（4）注意左、右互化，如求值：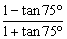
，可将式子化为：
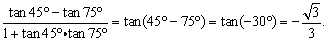
4、和（差）角的正、余弦公式的“加”、“减”、“乘”规律
（1）sin(α＋β)＋sin(α－β)=2sinαcosβ
（2）sin(α＋β)－sin(α－β)=2cosαsinβ
（3）sin(α＋β)·sin(α－β)=sin2α－sin2β
（4）cos(α＋β)＋cos(α－β)=2cosαcosβ
（5）cos(α＋β)－cos(α－β)=－2sinαsinβ
（6）cos(α＋β)·cos(α－β)=cos2α－sin2β
5、和（差）角的正切公式的变形形式
由tan(α＋β)=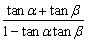
变形得
tanα＋tanβ＋tanαtanβtan(α＋β)=tan(α＋β)
由tan(α－β)=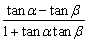
变形，
得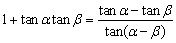
.
6、形如asinθ＋bcosθ的三角函数式可化成一个角的一个三角函数
即asinθ＋bcosθ=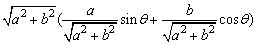
令
.
故asinθ＋bcosθ=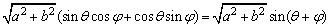
，
此即为化一公式，其中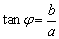
.
7、正弦、余弦、正切的和（差）角公式的联系
1、利用和、差角公式进行求值
例1、已知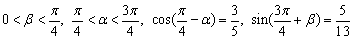
，求sin(α＋β).
分析：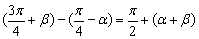
解析：
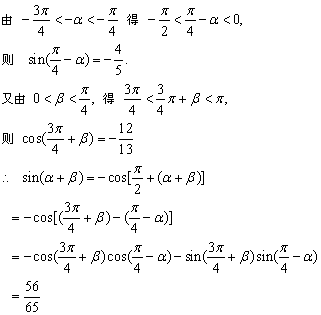
例2、已知
分析：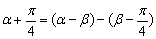
解析：
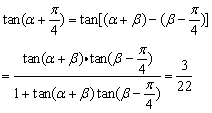
点评：
利用和（差）角公式进行求值时，一定要注意角的变换，另外还要注意公式的灵活运用，左右互化等.
2、利用和、差角公式进行化简
例3、化简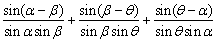
.
分析：将每个公式中分子用差角公式展开.
解析：原式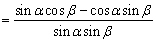
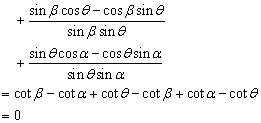
例4、化简：tanθ·tan2θ＋tan2θ·tan3θ＋…＋tan nθ·tan(n＋1)θ(n∈N＋).
分析：
问题实质是求数列{tankθ·tan(k＋1)θ}的前n项和，从通项入手，利用差角(k＋1)θ－kθ=θ的正切，产生tan(k＋1)θtankθ，再裂项求和.
解析：
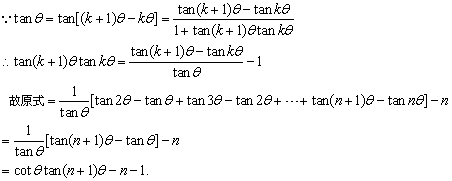
点评：
对于正切和（差）角公式有时常用它的变形形式：
tanα＋tanβ=tan(α＋β)(1－tanαtanβ)
tanα－tanβ=tan(α－β)(1＋tanαtanβ)
一般是指同一个式子中，既有两角的正切和（差），又有两角的正切积时用上述两公式进行变形较为简便.
3、利用和、差角公式进行证明
例5、求证：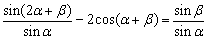
.
分析：2α＋β=（α＋β）＋α
证明：
左边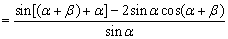
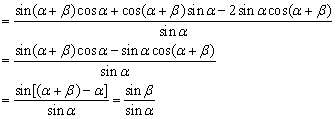
=右边
点评：等角变换，公式的左、右互化是解本题的关键.
例6、已知sin(2α＋β)=3sinβ，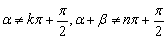
（k，n∈Z），
求证：tan(α＋β)=2tanα.
分析1：
由条件进行等角度换2α＋β=(α＋β)＋α，β=(α＋β)－α，利用和差角的正弦公式展开，化简得待证等式.
证明：∵ sin(2α＋β)=3sinβ
∴ sin[(α＋β)＋α]=3sin[(α＋β)－α]
sin(α＋β)cosα＋cos(α＋β)sinα=3sin(α＋β)cosα－3cos(α＋β)sinα
4cos(α＋β)sinα=2sin(α＋β)cosα
即 sin(α＋β)cosα=2cos(α＋β)sinα
∴ tan(α＋β)=2tanα．
分析2：
刚才的解法是从条件到结论.本题亦可用等价转换法证明，尤其是“观察到”条件中有系数“3”，故我们首先“关注”结论中的系数“2”．利用合分比定理，可“构造”出2来.
证明：
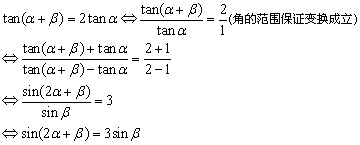
故命题成立.
点评：
①两个化切为弦关系很常用：
②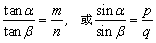
，这种结构，常联想实施合分比变换.
4、和、差角公式的综合运用
例7、求函数y=3sin(x＋20°)＋5sin(x＋80°)的最大值.
分析一：
由于涉及到的两角不一致，故可考虑利用和角公式先展开，然后再重新组合。
解：
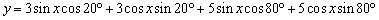
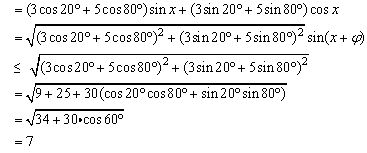
∴函数y=3sin(x＋20°)＋5sin(x＋80°)的最大值是7.
分析二：可把x＋20°作为整体.
解：令α= x＋20°，则x＋80°=α＋60°.
y=3sinα＋5sin(α＋60°)=3sinα＋5sinαcos60°＋5cosαsin60°
=
.
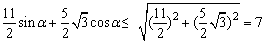∴函数y的最大值是7.
例8、 已知tanα、tanβ是方程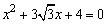
的两根，且
求α＋β的值．
分析： 由根与系数的关系联想到和角的正切公式来求解．
解析：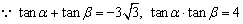
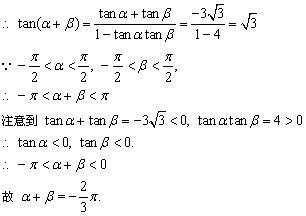
点评： 本题既要注意到α＋β的取值范围，又要善于发掘隐含条件tanα＜0，tanβ＜0．
例9、求值：（1＋tan1°）（1＋tan2°）…（1＋tan44°）．
分析：利用两角和的正切公式的变形，
tanα＋tanβ=tan(α＋β)(1－tanαtanβ)．
解析：∵（1＋tan1°）（1＋tan44°）
=1＋（tan1°＋tan44°）＋tan1°tan44°
=1＋tan（1°＋44°）（1－tan1°tan44°）＋tan1°tan44°
=1＋tan45°（1－tan1°tan44°）＋tan1°tan44°
=1＋（1－tan1°tan44°）＋tan1°tan44°
=2
同理可求得（1＋tan2°）（1＋tan43°）=2……
∴原式=222
点评：
注意到1°＋44°=45°，2°＋43°=45°，…，利用和角的正切公式变形是解题的切入点．
