1、数列的前n项和的求法
例1、求和.
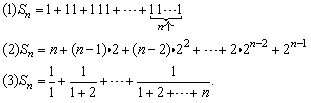
分析：
（1）考察右边第k项为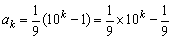
，它可以看作等比数列{10n}与常数列{
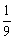}的差，可采用集项求和法（所谓集项是指将有规律的项放在一起）.
（2）将和式看作数列的前n项，则此数列的第k项为(n－R＋1)2R－1，可考虑用错位相减法求和，将Sn乘以2减去Sn后用等比数列的前n项和公式.
（3）将和式看作数列的前n项，考察此数列的第k项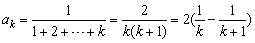
，可用裂项相消法求和.
解答：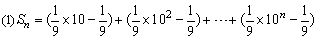
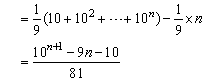
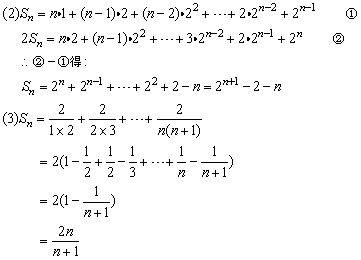
小结：
1、如果一个数列的项可以表示成一个等差（等比）数列与另一个等比数列的和或差，可用集项求和法求和.
2、如果一个数列的项可以表示成一个等差数列与一个等比数列（公比不为1）的对应项的积可由错位相减法进行求和.
3、如果一个数列的项可以表示成两个数之差，且能产生正负相消的项，可考虑用裂项求和法.
例2、设数列{an}的前n项和为Sn，且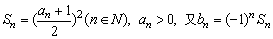
，求数列{bn}的前n项和Tn.
分析：由Sn与an的关系可求出an或Sn，求出bn．分析bn的组成，选择适当方法求和.
解答：
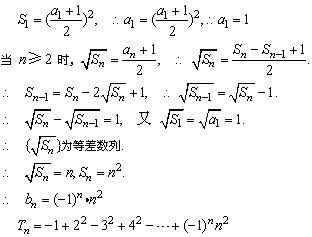
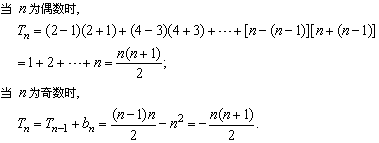
小结：
数列中如出现(－1)n时，可考虑正、负项结合，或单正项求和，单负项求和.
2、数列的通项的求法
例3、已知数列{an}满足
，求数列{an}的通项公式.
解法一：
用n－1换条件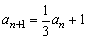
中的n，得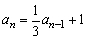
（n≥2），作差得
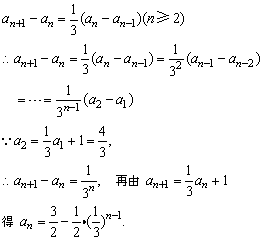
解法二：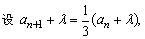
小结：
一般地，形如an＋1=pan＋q(qp≠0,q≠1)的递推关系式给出的数列，可考虑以上两种方法求通项.
例4、根据下列条件，分别求出数列{an}的通项公式.
（1） 
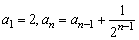（n≥2）；
（2） （2000年全国高考题）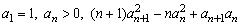
=0（n∈N）.
解答：（1）由题知，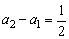
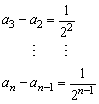
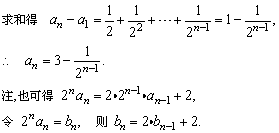
由例1中的方法求出bn即可得an.
（2）由条件知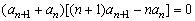
，
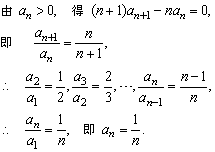
小结：
形如an＋1－an=f(n)的递推关系式给出的数列可考虑用累加法求通项，形如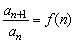
的递推关系式给出的数列可考虑用累积法求通项.
3、关于分期付款的计算问题
分期付款中的有关规定：
（1）在分期付款中，每期的利息均按复利计算；
（2）分期付款中，每期所付款额相同；
（3）在分期付款时，商品售价和每期所付款额在货款全部付清前会随着时间的推移而增加；
（4）各期所付款额连同最后一期付款时所付款额本利之和等于商品售价从购买到最后一期付款时的本利和．
分期付款的计算：
设商品售价a元，分n个月付清，月息为p，这样有二种思考方式；
（1）可以把分期付款理解为零存整取，到最后一次付款时，一次性冲掉应付款和利息.
设每月等额还x元，则有等式
x＋x(1＋p)＋x(1＋p)2＋…＋x(1＋p)n－1=a(1＋p)n.
（2）还可以理解为每次付款后冲掉部分应付款及相应利息.
设每次还x元，每次还款后欠款所组成的数列为{an}，则有
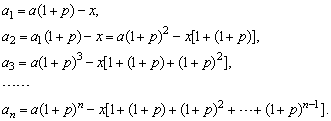
令an=0，则化归为第1种情况，因此两种思路殊途同归.
一般数列应用题首先应建立适当的数列，然后可以先写出具体的几项以加深对题意的理解，并发现规律，有的题目可以建立递推关系式．
例5、某人的购房总额为72000元，首付43200元，余下28800元分10年还清．按年利7.5%计息，并且每年复利计算一次，那么每年应付款为多少元？（精确到百元）
解法一：
按第1种思路，设每年还款x元，则有
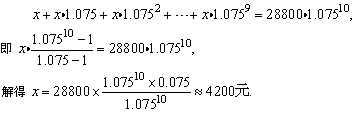
解法二：
按第2种思路，设每年还款x元，每次还款后欠银行的钱数构成数列{an}，则
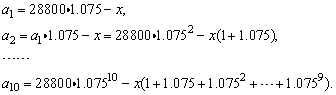
令 a10=0，解得x≈4200元．
小结：
解数列应用题关键是如何将实际问题转化为数学问题，而建立正确的数学模型．通常是依据题意直接建立等差，等比数列模型或依据题意得到某种递推关系，再转化为等差、等比数列模型，从而利用两类特殊数列的性质达到解决问题的目的.
