|
一、一周知识概述
本周主要学习了同角三角函数基本关系式及其应用.同角三角函数基本关系式指: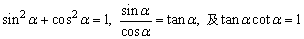 ,利用这三个基本关系式,可以根据一个角的正弦、余弦、正切、余切中的一个值求出其余三个值,还可以进行化简与证明. ,利用这三个基本关系式,可以根据一个角的正弦、余弦、正切、余切中的一个值求出其余三个值,还可以进行化简与证明.
二、重点知识讲解
1、同角三角函数基本关系式:同角三角函数基本关系可概括为平方关系,商数关系和倒数关系,如考虑sinα,cosα,tanα,cotα与secα,cscα六个函数,还可借助如下图表形象记忆:
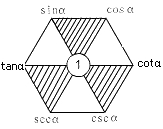
(1)对角线上两个函数的积为1(倒数关系)
(2)任一顶点的函数等于与其相邻两个顶点的函数的积(商数关系)
(3)阴影部分,顶角两个函数的平方和等于底角函数的平方(平方关系)
由此图可得出公式的变形形式或其他同角函数关系式如:
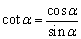 ,1+tan2α=sec2α,1+cot2α=csc2α, ,1+tan2α=sec2α,1+cot2α=csc2α,
sinαcscα=1,cosα·secα=1等.
例1、下列结论中能成立的是( )
A.sinα=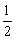 且cosα= 且cosα=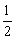
B.tanα=2且cotα=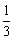
C.tanα=1且cosα=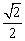
D.sinα=1且tanα·cosα=1
[解析]
2、已知某角的一个三角函数值,求此角的其他三角函数值.这类题型主要有如下三类:
(1)已知某角的某一三角函数值,且知角的象限;
(2)已知某角的某一三角函数值,不知角的象限;
(3)已知某角的某一三角函数值为字母,不知角的象限,对于(2)(3)两类,应注意分情况讨论.
例2、已知cotα=m(m≠0),求cosα.
[解析]
3、运用基本关系式进行化简或求值.
例3、(1)α是第三象限角,化简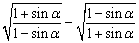 ; ;
(2)若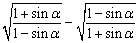 =2tanα,求α的范围. =2tanα,求α的范围.
[解析]
例4、化简或求值:
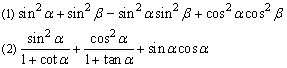
[解析]
例5、已知 ,求sin2α+sinαcosα+cos2α的值. ,求sin2α+sinαcosα+cos2α的值.
[解析]
4、运用同角三角关系式进行证明
恒等式与条件等式的证明可以用作差法,分析法,可以考虑“化繁为简”、“切割化弦”,也可考虑“从左到右”、“从右到左”、“两边归一”.
例6、求证:tan2θ-sin2θ=tan2θsin2θ.
[解析]
例7、已知asecθ-xtanθ=y,bsecθ+ytanθ=x.
求证:x2+y2=a2+b2.
[解析]
三、难点知识剖析
基本关系式的逆向使用和变形使用,以及对条件的合理变形和整体代替是本节知识的难点.
例8、已知tan2θ=1+2tan2φ,求证:sin2φ=2sin2θ-1.
[解析]
例9、已知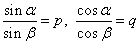 ,且P≠±1,q≠0,求tanαtanβ的值. ,且P≠±1,q≠0,求tanαtanβ的值.
[解析]
|