一、一周知识概述

本周主要是学习正弦函数、余弦函数的图象和性质．

二、重难点讲解

1、正弦、余弦函数的图像和性质

2、函数y=sinx,x∈[0,2π]图象上五个关键点：

函数y=cosx, x∈[0,2π]图象上五个关键点：

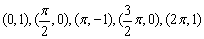
正（余）弦函数图像的作法通常采用“五点法”作图：

　　选取正（余）弦函数的一个周期（一般取x∈[0，2π]，根据五个关键点（其横坐标分别为0、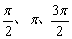、2π）分别找到函数图像的最高点、最低点及其与x轴的交点，从而基本确定了函数的图像位置与形状，再把上述简图沿x轴向左或向右连续地平行移动，每次移动的距离为2π，即可得到函数y=sinx，x∈R和y=cosx，x∈R的图像——正弦曲线和余弦曲线．

3、周期函数的定义：对于函数y=f(x)，如果存在一个非零常数T，使得x取定义域内的任意值时，都有f(x＋T)=f(x)，那么函数y=f(x)叫做周期函数，其中非零常数T叫这个函数的一个周期．如果T中存在一个最小的正数，那么这个最小正数叫做这个函数的最小正周期，以后提到的周期T，一般均是指最小正周期．周期函数的定义可以理解为：当函数对于自变量的一切值每增加或减少一个非零定值T时，函数值重复出现，定义中“x取定义域内的每一个值”和“不为零的常数”是两个不可缺少的条件．正弦函数和余弦函数都是周期函数，2kπ（k∈Z且k≠0）都是它们的周期，且最小正周期为2π．

　　对于周期函数应注意以下几点：

　　（1）一般地，如果T（T>0）是函数y=f(x)的一个周期，那么kT(k∈N*)也是函数y=f(x)的周期；

　　（2）一个周期函数未必都有最小正周期，例如常数函数y=c，就不存在最小正周期；

　　（3）对于函数y=f(ωx)(ω≠0)，如果存在非零常数T，使得f(ωx＋T)=f(ωx)对定义域的任何值都成立，那么这个函数的一个周期是．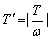

　　4、正（余）弦函数在其定义域内都不是单调函数，但存在单调区间，如y=sinx在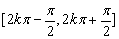（k∈Z）上是增函数，注意不能说正弦函数在第一、四象限内为增函数，例如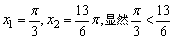：且均为第一象限角，但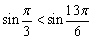不能成立．

三、例题讲解

1、作出下列函数的简图：

（1）y=2cosx＋1，x∈[0，2π]

（2）y=sin|x|，x∈[－2π，2π]．

[解析]

2、求函数的定义域．

[解析]

3、求下列函数的单调递增区间：

[解析]

4、判断函数上的奇偶性．

[解析]

5、求下列函数的周期：

[解析]

6、求下列函数的值域：

[解析]

7、已知函数上的最大值为1，求实数a的值．

[解析]

8、如果函数y=f(x)=sin2x＋acox2x的图象关于直线对称，试求a的值.

[解析]