|
一、一周知识概述
先通过能的概念引入动能概念,决定动能的因素,利用功和能的关系,推导出动能定理,正确理解定理的含义,明确动能定理的解题步骤,通过习题课,提高学生应用定理解决问题的能力。
二、重难点知识归纳与讲解
1、动能
(1)EK为状态量;
(2)EK为标量,动能求和为代数和;
(3)EK为相对量(一般相对地面的动能)。
2、动能定理
(1)ΣW为过程量;△EK为状态量之差。
(2)ΣW为功的代数和(做功不分先后,按代数和计算)。
(3)定理对于恒力做功,对于变力做功均成立。若为变力做功,可用物体的初末状态的动能变化来量度变力做功的大小。这正是用动能定理解题较动力学方法简捷之处。
3、应用动能定理解决问题的步骤
(1)确定研究对象是一物体或系统;
(2)分析受力情况以便确定各力做功情况;
(3)分析物体或系统的初、末状态的动能;
(4)应用动能定理求解。
三、典型分析
例1、如图所示,固定的光滑竖直杆上套着一个滑块,用轻绳系着滑块绕过光滑的定滑轮,以大小恒定的拉力F拉绳,使滑块从A点起由静止开始上升.若从A点上升至B点和从B点上升至C点的过程中拉力F做的功分别为W1、W2,滑块经B、C两点时的动能分别为EkB、EkC,图中AB=BC,则一定有( )

A.W1>W2 B.W1<W2
C.EkB>EkC D.EkB<EkC
答案:A
解析:
由图可分析出,从A到B过程中绳端移动的距离△s1大于从移到C过程中,绳端移动的距离△s2.
据W1=F△s1,W2=F△s2,可知W1>W2.
因F大小未知,则物体由A到C的过程是加速、减速情况难以确定.故A项正确.
例2、某人造卫星运动的轨道可近似看作是以地心为中心的圆.由于阻力作用,人造卫星到地心的距离从r1慢慢变到r2,用Ek1、Ek2分别表示卫星在这两个轨道上的动能,则( )
A.r1<r2,Ek1<Ek2 B.r1>r2,Ek1<Ek2
C.r1<r2,Ek1>Ek2 D.r1>r2,Ek1>Ek2
答案:B
解析:
卫星因为阻力作用而损失机械能,运转轨道半径减小,即r1>r2.根据线速度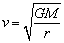 ,速度增大,故Ek1>Ek2,则B项正确. ,速度增大,故Ek1>Ek2,则B项正确.
例3、如图所示,半径R=0.40 m的光滑半圆环轨道处于竖直平面内,半圆环与粗糙的水平地面相切于圆环的端点A.一质量m=0.10kg的小球,以初速度v0=7.0m/s在水平地面上向左做加速度a=3.0m/s2的匀减速直线运动,运动4.0 m后,冲上竖直半圆环,最后小球落在C点.求A、C间的距离(取重力加速度g=10m/s2).

答案:1.2m
解析:
匀减速运动过程中,有:vA2-v02=-2as ①
恰好做圆周运动时物体在最高点B满足:mg=
vm=2m/s ②
假设物体能到达圆环的最高点B,由机械能守恒: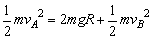 ③ ③
联立①③可得vB=3m/s
因为vB>vm,所以小球能通过最高点B.
小球从B点做平抛运动,有:2R=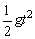 ④ ④
SAC=vB·t ⑤
由④⑤得:SAC=1.2m ⑥
例4、如图所示,用半径R=0.10m的轮轴,通过跨在定滑轮上的细绳,拉一个放在倾角为5.7°的斜面上,质量m=2kg的物体。开始时物体静止在A点,这时绳与斜面的夹角α1=30°,后来把物体拉到B点,这时绳与斜面的夹角α2=60°.轮轴转动的角速度ω=5rad/s,定滑轮与斜面相距h=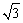 m,物体与斜面间所受的平均阻力f=2N.已知sin5.7°=0.10,cos5.7°=0.99.求: m,物体与斜面间所受的平均阻力f=2N.已知sin5.7°=0.10,cos5.7°=0.99.求:
(1)物体通过B点时的速度;
(2)物体从A到B过程中绳对物体所做的功。

解析:
(1)应用运动的合成与分解知识,绳的速度不等于物体沿斜面移动的速度。
沿绳方向的速度v绳=ωR=5×0.10=0.5(m/s).
物体沿斜面的速度是合速度,沿绳方向的速度为分速度,它们之间的关系如图所示,即:

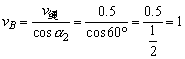 (m/s) (m/s)
同理可得,物体经过A点时速度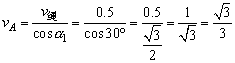 (m/s) (m/s)
(2)物体从A点运动到B点,受力分析如图所示,

由动能定理得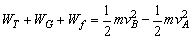 , ,

例5、质量为M的列车在平直的轨道上匀速行驶,忽然尾部有一节质量为m的车厢脱钩,待司机发现并关闭发动机时,前部车厢已驶过的距离为L。已知列车受到的阻力与质量成正比,发动机工作时牵引力不变。求前后两部分都停止时,两部分间的距离。
解析:
根据题意,先画出运动情景图,分析运动过程,找出各过程中的做功情况与能量变化情况。

依题意,列车牵引力F=μMg ①
对车厢m:-μmgS1=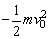 ② ②
对机车(M-m):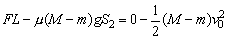 ③ ③
x=S2-S1 ④
由上式各式得
本题也可用牛顿运动定律与运动学公式求解,但较上述方法烦。
最简捷的方法为“补偿法”。
假设车厢脱钩时立即发现,两车将以相同加速度a=μg减速运行,其初速v0与末速vt=0均相同。
故相对位移为0,对地位移均为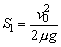 。 。
现机车比车厢多行x,要多克服摩擦阻力做功,即μ(M-m)gx=W阻,是由于司机未发现前牵引力做功来补充其能量.
有μ(M-m)gx=FL=μMgL.
∴ 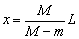 。 。
- 返回 -
|