|
一、一周知识概述
利用动量守恒定律分析了反冲运动,介绍了火箭飞行原理,从动量和能量观点介绍了研究一维碰撞问题的基本方法、完成了验证动量守恒定律的学生分组实验。
二、重难点知识归纳与讲解
1、反冲运动
(1)反冲运动:两个物体相互作用,由于一个物体的运动,而引起另一个物体的反退运动。如原来静止的大炮,向前发射炮弹后,炮身要后退,炮身的后退就是反冲运动,再如,发射火箭时,火箭向下高速喷射气体,使火箭获得向上的速度,这也是反冲运动。
(2)反冲运动遵循的规律:反冲运动是系统内力作用的结果,虽然有时系统所受的合外力不为零,但由于系统内力远远大于外力,所以系统的总动量守恒。此外,如系统所受外力的合力不为零,但在某一方向上不受外力或在该方向上所受外力的合力为零,则在该方向上的动量(即总动量在该方向上的分量)是守恒的,这种某方向上的动量守恒应用很广泛。
2、火箭原理
火箭是反冲运动的重要应用,它是靠喷出气流的反冲作用而获得巨大速度的。现代火箭主要由壳体和燃料两大部分组成,壳体是圆筒形的,前端是封闭的尖端,后端有尾喷管,燃料燃烧时产生的高温高压气体以很大的速度从尾部向后喷出,火箭就向前飞去。
火箭向前飞行所能达到的最大速度,也就是燃料烧尽时火箭获得的最终速度,它跟什么因素有关呢?根据动量守恒定律,理论上的计算表明,最终速度主要取决于两个条件,一是喷气速度,二是质量比,即火箭开始飞行时的质量与燃料烧尽时的质量之比,喷气速度越大,质量比越大,火箭的最终速度也越大。为了提高喷气速度,需要使用高质量的燃料,目前常用的液体燃料是液氢,用液氧做氧化剂,质量比与火箭的结构和材料有关,现代火箭能达到的质量比不超过10.在现代技术条件下,一级火箭的最终速度还达不到发射人造卫星所需要的速度。所以,要发射卫星,必须采用多级火箭。
3、碰撞
相对运动的物体相遇,在极短时间内,通过相互作用,运动状态发生显著变化的过程叫碰撞
(1)分析碰撞问题的方法
①碰撞时间忽略不计。
②碰撞过程系统动量守恒P1+P2=P′1+P′2
③碰撞后系统动能小于(或等于)碰撞前系统动能

④碰撞前后速度要满足一定关系
如果碰前两物体同向运动,则后面物体速度必大于前面物体速度,否则无法实现追及碰撞,碰后原来运动在前面的物体速度一定增大,因为此物体碰撞时受冲量与其初速度方向相同。
如果碰撞后两物体同向运动,则前面物体速度必大于或等于后面物体速度,否则碰撞尚未结束。
三、典例分析
例1、甲、乙两球在光滑水平轨道上同向运动,已知它们的动量分别是p甲=5 kg·m/s,p乙=7 kg·m/s.甲追乙并发生碰撞,碰后乙球的动量变为p′乙=10 kg·m/s,则两球质量m甲与m乙的关系可能是( )
A.m甲=m乙
B.m乙=2m甲
C.m乙=4m甲
D.m乙=6m甲
点拨:
由碰撞中动量守恒可求得p′甲=2kg·m/s.要使甲追上乙,则必有:
v甲>v乙,即
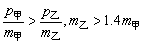 ① ①
碰后p′甲、p′乙均大于零,表示同向运动,则应有:v′乙≥v′甲,即
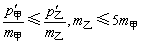 ② ②
碰撞过程中,动能不增加,则
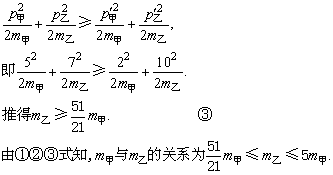
正确答案应选C
例2、如图所示,光滑水平面上,质量为m的小球B连接着轻质弹簧,处于静止状态.质量为2m的小球A以大小为v0的初速度向右运动,接着逐渐压缩弹簧并使B运动,过一段时间,A与弹簧分离.
(1)当弹簧被压缩到最短时,弹簧的弹性势能Ep多大?
(2)若开始时在B球的右侧某位置固定一块挡板,在A球与弹簧末分离前使B球与挡板发生碰撞,并在碰后立刻将挡板撤走.设B球与挡板的碰撞时间极短,碰后B球的速度大小不变但方向相反.欲使此后弹簧被压缩到最短时,弹性势能达到第(1)问中Ep的2.5倍,必须使B球在速度多大时与挡板发生碰撞?

解:
(1)当弹簧被压缩到最短时,A、B速度相等,2mv0=3mv1.
A和B的共同速度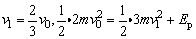
此时弹簧的弹性势能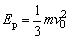 . .
(2)B碰挡板时没有机械能损失,碰后弹簧被压缩到最短时,A、B速度也相等,
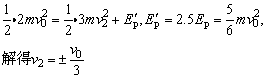
取向右为正方向.若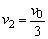 ,则表示B球与板碰撞后,A、B此时一起向右运动. ,则表示B球与板碰撞后,A、B此时一起向右运动.
B球与板碰撞前B与A动量守恒,2mv0=2mvA+mvB①
B球与板碰撞后B与A动量也守恒,2mvA-mvB=3mv2=3m·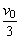
解得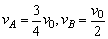 ,因为此时vA>vB,弹簧还将继续缩短,所以这种状态是能够出现的. ,因为此时vA>vB,弹簧还将继续缩短,所以这种状态是能够出现的.
若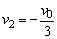 ,则表示B球与板碰撞后A、B向左运动,B球与板碰撞后B和A动量守恒, ,则表示B球与板碰撞后A、B向左运动,B球与板碰撞后B和A动量守恒,
2mvA-mvB=3mv2=-3m·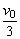 ② ②
由①②式可得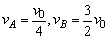 .此时A、B球的总动能 .此时A、B球的总动能
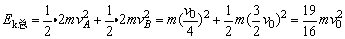 , ,
Ek总大于A球最初的动能mv02,因此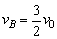 这种状态是不可能出现的.因此,必须使B球在速度为 这种状态是不可能出现的.因此,必须使B球在速度为 时与挡板发生碰撞. 时与挡板发生碰撞.
例3、一火箭喷气发动机每次喷出m=200g的气体,气体离开发动机喷出时的速度v=1000m/s,设火箭质量M=300kg,发动机每秒喷气20次。
(1)当第三次气体喷出后,火箭的速度多大?
(2)运动第1秒末,火箭的速度多大?
解析:
火箭喷气属反冲现象,火箭和气体系统动量守恒,运用动量守恒定律求解.
喷出气体运动方向与火箭运动方向相反,系统动量可认为守恒.
第一次气体喷出后,火箭速度为v1,有(M-m)v1-mv=0.
∴ . .
第二次气体喷出后,火箭速度为v2,有(M-2m)v2-mv=(M-m)v1.
∴ . .
第三次气体喷出后,火箭速度为v3,有(M-3m)v3-mv=(M-2m)v2.
∴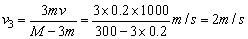 . .
依此类推,第n次气体喷出后,火箭速度为vn,有
(M-nm)vn-mv=[M-(n-1)m]vn-1.
∴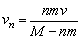
因为每秒喷气20次,所以1s末火箭速度为

例4、光滑水平面上有A、B两辆小车,mB=1kg,原来静止,mA=1kg(含支架)。现将小球C用长为0.2m的细线悬于支架顶端,mC=0.5kg.开始时A车与C球以v0=4m/s的速度冲向B车,如图所示,若A、B正碰后粘在一起,不计空气阻力,g取10m/s2,试求小球C上摆的最大高度.
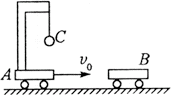
解析:
设A、B相碰后二者的共同速度为v,由动量守恒定律得:mAvA=(mA+mB)v
解得v=2m/s
A、B粘在一起后,小球C向右摆,细绳在水平方向分力使A、B加速,当C的速度与A、B水平方向的速度相同时小球摆至最高点,则由动量守恒定律有:
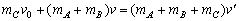 . .
解得A、B、C相同的速度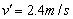 . .
再由机械能守恒定律,设C球上摆的最大高度为h,则:
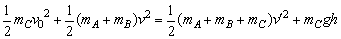 . .
解得h=0.16m.
答案:h=0.16m.
- 返回 -
|