|
一、一周知识概述
先从重力做功引入重力势能的概念以及重力功与重力势能变化量的关系。在只有重力或弹力做功的情况下,由动能定理推出机械能守恒定律内容,进而分析其守恒条件以及其应用。
二、重、难点知识归纳与讲解
1、重力势能(Ep)
①大小 Ep=mgh.
②Ep为标量,其正负是相对零势能面的高、低而言。
③Ep为相对量,零势能面选取不同,其重力势能不同,但重力势能的变化则与零势面选取无关。
④重力势能单位:焦耳
2、重力功与重力势能变化:(如图)
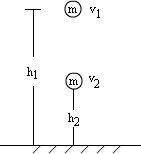
(1)重力势能变化总等于重力功大小。WG=△EP=mg(h1-h2)=mgh1-mgh2.
(2)重力功大小与路径无关,只由起点与终点在重力方向上位移决定。
3、机械能守恒定律
(1)内容:在只有重力或弹力做功的情况下,物体系内动能与势能(重力势能、弹力势能)发生相互转化,但物体系内机械能总量保持不变。
(2)表达式:E=E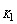 +E +E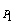 =E =E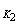 +E +E =…恒量 =…恒量
或 △E=0
(3)守恒条件:只有重力或弹力做功。(系统)

(4)解题步骤:
①选取研究对象(物体系)
②明确研究对象运动过程,分析各力做功情况,判定是否满足守恒条件。
③恰当选取参考面,确定初末状态机械能。
④依守恒定律列方程,进行求解。
三、典例分析
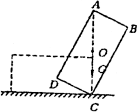
例1、一个质量分布均匀的长方形木块,放在粗糙的水平地面上,长为2a,宽为a。若要把它从图中所示的位置直立起来,外力至少要做多少功?
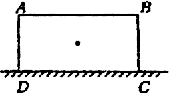
解析:
本题是求变力做功的问题,应该用功能关系求解。把木块直立起来外力做的功至少等于物块重力势能的增量。而若使外力做的功最少,应是木块的重心O升至C点正上方,如图所示。在此过程重心升高:h=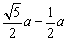 ,所以外力最少对木块做功W=mgh= ,所以外力最少对木块做功W=mgh=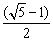 ·mga ·mga
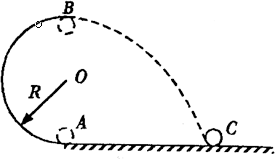
例2、如图所示,半径为R,光滑的半圆轨道与地面垂直,一小球经过最高点飞出后,落在水平面上的C点,测出AC=2R,求小球自A点进入轨道时的速度大小。
解析:
小球在轨道上运动的过程中,小球受重力、轨道对它的压力,由于轨道对它的压力时时刻刻与速度的方向垂直,因而压力对小球不做功,小球离开轨道后,做平抛运动,因此小球由A到B到C的整个过程中,机械能守恒。先由平抛运动的知识求出小球经过B点时的速度,然后由机械能守恒定律求出小球在A点时的速度。
解:
由平抛运动的知识有2R=vBt 2R=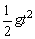 解得vB= 解得vB=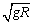
以小球和地球组成的系统为研究对象,选择水平面所在的平面为参考平面,以小球经过A时为初状态,经过B时为末状态,由机械能守恒定律有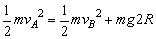 vA= vA=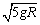
讨论:若将轨道改为半圆形弯管,为使小球能达到B点,则从A点进入时速度又为多大?(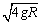 )。 )。
例3、一条长为L的铁链置于光滑水平桌面上,用手按住一端,使另一端长为L1的一段下垂于桌边,如图所示,放手后铁链下滑,则当铁链全部通过桌面的瞬间,铁链具有的速率为多大?
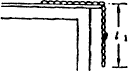
解析:
系统内只有重力做功,故机械能守恒,以链条左端离开桌边时末状态,且以链条重心为零势能面,则
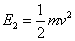 单位长度质量为 单位长度质量为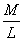
E2=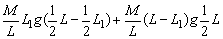
E1=E2∴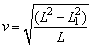
例4、在长为2L的轻杆的一端和中点各固定一个小球A和B.A、B两球的质量均为m,将轻杆拉至水平,由静止释放,让杆绕O点转动,不计空气阻力,当轻杆转至竖直方向时,求:
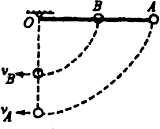
(1)A、B两球的速度vA、、vB;
(2)在上述过程中轻杆对A球所做的功W。
解析:
(1)A球和B球单独随轻杆在空间转动时,它们的快慢程度是不相同的,也就是说,A、B球和轻杆一起转动的过程中,轻杆对A、B球是做功的。因此,A、B球的机械能不守恒,只有以AB球为物体系时,机械能才守恒(此时杆对A、B球所做的功为内力的功),根据机械能守恒定律列出方程。
mg·2L+mg·2L=mgL+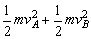 (1) (1)
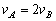 (2) (2)
所以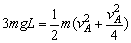
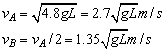
(2)若A球单独随轻杆摆下,转至最低点时
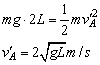
所以轻杆对A球所做的功W为
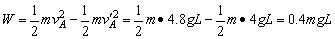
例5、在一个半径为R的半圆形轨道边缘上固定着一个定滑轮,一轻绳两端分别连着质量为m1和 m2的物体挂在定滑轮两边,且m1> m2,开始时m1、m2均静止,放手后m1将从半圆环轨道边缘处滑下。m1、m2可看作质点,轨道固定在桌子边上不动,如图所示。
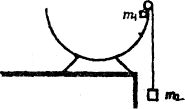
(1)求m1经过圆形轨道最低点时的速度;
(2)为使m1能够到达最低点,m1与m2之间满足什么关系?
解析:

m1运动到轨道最低点时速度为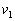 ,将其分解如图所示。由m1、m2组成的系统的机械守恒得 ,将其分解如图所示。由m1、m2组成的系统的机械守恒得  由图可知 由图可知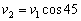 ° °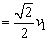 , ,
∴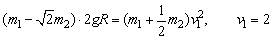 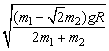 , ,
要使m1能到达最低点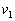 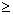 0, 0,
即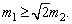
- 返回 -
|