|
一、一周知识概述
1、通过学习知道描述匀速圆周运动的几个物理量有:线速度、角速度、周期、频率以及它们之间的关系。
2、由速度方向的改变快慢,引入向心加速度、向心力。
3、知道向心力为效果力,从而在具体实例中如何寻找向心力的来源。
二、重难点归纳与讲解
1、角速度与线速度之间的关系v=ωr
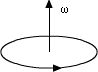
(1)线速度为变量(匀速圆周运动指速率不变)。角速度的恒量,其方向遵循右手螺旋法则。这一点高中教材未涉及,但课本习题将涉及到这一点。
(2)当ω一定v∝r,当v一定,ω∝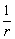 。 。
2、周期与频率之间的关系
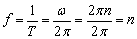 (转/秒) (转/秒)
在国际单位中角速度用rad/s
3、向心加速度与向心力
(1)向心加速度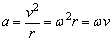
①其大小反映了速度方向变化的快慢,由于v⊥a,故不能改变速度大小。
②a与r的关系如图所示,
A为ω不变,a∝r,B为v不变,a∝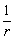 . .

(2)向心力: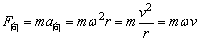
①F向为效果力,只要能维持物体作圆运动的力,都能称向心力,如摩擦力、弹力、引力、合力或分力。
②对于匀速圆周运动,向心力大小不变,但方向时刻改变,故匀速圆周运动为变速运动。
4、匀速圆运动的两个实例
(1)汽车过凸桥。
(2)火车转弯。
实例典型,应从中体会到找向心力来源的方法,进一步提高应用牛顿定律的解题能力。
三、典型例题分析
例1、如图所示,悬挂在小车支架上的摆长为l的摆,小车与摆球一起以速度v0匀速向右运动.小车与矮墙相碰后立即停止(不弹回),则下列关于摆球上升能够到达的最大高度H的说法中,正确的是( ).
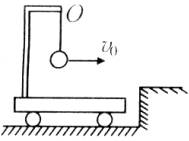
A.若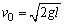 ,则H=l ,则H=l
B.若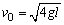 ,则H=2l ,则H=2l
C.不论v0多大,可以肯定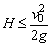 总是成立的 总是成立的
D.上述说法都正确
解析:
(1)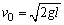 时, 时,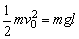 ,H=l.球到达A点时,速度为零,随后沿原路返回.A正确. ,H=l.球到达A点时,速度为零,随后沿原路返回.A正确.
(2) 时, 时,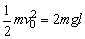 ,但小球不能上升到2l的高度,因为小球过B点条件是 ,但小球不能上升到2l的高度,因为小球过B点条件是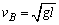 . .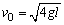 时,摆球先沿圆周上升到C点,一定存在着这样一个C点,小球到达C点时,细线中的拉力恰好减小到零,随后小球斜上做“斜抛”运动,到达最高点时竖直方向的分速度为零,但水平方向的分速度不为零,即小球到达最高点时动能不为零;根据机械能守恒定律,小球的机械能总量为 时,摆球先沿圆周上升到C点,一定存在着这样一个C点,小球到达C点时,细线中的拉力恰好减小到零,随后小球斜上做“斜抛”运动,到达最高点时竖直方向的分速度为零,但水平方向的分速度不为零,即小球到达最高点时动能不为零;根据机械能守恒定律,小球的机械能总量为 ,它到达最高点时动能不为零,则其重力势能一定小于2mgl,即它能到达的最大高度肯定小于2l.所以,选择项B、D都错. ,它到达最高点时动能不为零,则其重力势能一定小于2mgl,即它能到达的最大高度肯定小于2l.所以,选择项B、D都错.
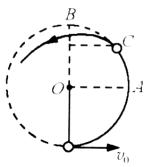
(3)根据机械能守恒定律,显然 ,只有小球到达最高点,速度为零时才有 ,只有小球到达最高点,速度为零时才有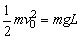 .所以不管v0多大, .所以不管v0多大, 总是正确的.C正确. 总是正确的.C正确.
答案:AC
例2、如图所示,质点P以O为圆心做匀速圆周运动,运动半径为R,周期为T,当质点过图中位置的瞬间,另一质量为m的质点受力F而开始做直线运动,它的初速度为零.为使上述两质点能在某时刻速度相同,则力F必须满足什么条件?

解析:
两质点速度相同,既要大小相同,方向也要同方向.因此质点P只有运动到图中a点的位置才能与m的质点速度相同,即从b点位置开始计时,运动时间应满足
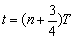 (n=0,1,2,……) (n=0,1,2,……)
m匀变速直线运动有F=ma ①
v=at ②
P质点匀速圆周运动v=2πR/T ③
①②③联立得F=m2πR(Tt).将t代入得
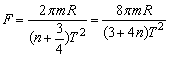
例3、轻杆一端固定在光滑水平轴O上,另一一端固定一质量为m的小球,如图所示,给小球一初速度,使其在竖直平面内做圆周运动,且刚好能通过最高点P.下列说法正确的是( )
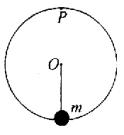
A.小球在最高点时对杆的力为零
B.小球在最高点时对杆的作用力大小为mg
C.若增大小球的初速度,则在最高点时球对杆的力一定增大
D.若增大小球的初速度,则在最高点时球对杆的力可能增大
解析:
首先要分析题意中“刚好能通过最高点P”这一隐含条件,它说明此时的向心力为在P点所可能取的向心力中的最小值,在P点杆对小球可能是支持力.可能是压力,可能无作用力.当杆对小球是支持力且等于mg时,向心力达最小值为零,因此B对.
增大小球的初速度,由机械能守恒定律,小球达P点速度vP也要增加,但vP仍小于以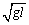 时,杆对球是支持力,对球 时,杆对球是支持力,对球
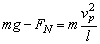 . .
随着vP增大,FN减小,即球对杆的作用力也减小.vP>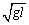 时,杆对球是拉力,对球 时,杆对球是拉力,对球
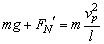 . .
随着增vP大, FN′增大,即球对杆的作用力也增大,D对.
答案:BD
例4、如图,长为L的轻杆,两端各连接一个质量都是m的小球,使它们以轻杆中点为轴在竖直平面内做匀速圆周运动,周期为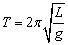 。求它们通过竖直位置时杆分别对上下两球的作用力。 。求它们通过竖直位置时杆分别对上下两球的作用力。
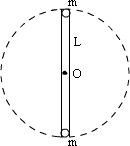
解析:
由转动周期可求出小球转动角速度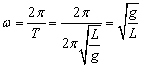
设上端小球受到杆的拉力,则方向与重力相同
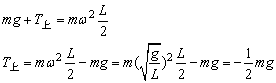
负号说明与所设方向相反,即上端小球受到杆的支持力,方向向上。
设下端小球受到杆的拉力,方向向上。
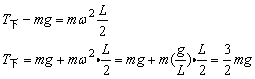
正号说明与所设方向相同。
例5、“东风”汽车公司在湖北某地有一试车场,其中有一检测汽车在极限状态下车速的试车道,呈碗状,如图,设某小汽车在A车道上飞驰,该车逆转弯半径为R=150m,路面倾角θ=45°,路面与车胎间摩擦因数μ=0.25,求该车最大车速度不得超过多少?
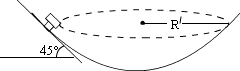
解析:
隔离车:分析受力情况:由于最大车速时,车受摩擦力方向沿路面斜向下。
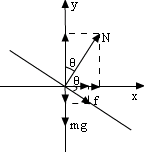

- 返回 -
|