|
一、一周知识概述
在前面已经讲过的解决问题的方法:隔离法、正交分解法的基础上,本周通过习题课的讲述,进一步讨论力的瞬时性,应用中临界条件的寻找,超重与失重的分析,进一步掌握好牛顿运动定律。
二、重难点知识讲解
1、由F=ma可知a与F有瞬时关系,即a与F同时产生,同时增减,同时消失,a可突变,但速度v不能突变。
2、寻找临界条件时,必须先认真分析物理过程,力的变化与相关的运动量变化之间的关系,寻找转折点。
3、超重与失重的条件

例1、如图所示,已知质量为m的木块在大小为T的水平拉力作用下,沿粗糙水平面做匀加速直线运动,加速度为a,则木块与地面之间的动摩擦因数为______.若在木块上再施加一个与水平拉力T在同一竖直平面内的推力,而不改变木块加速度的大小和方向,则此推力与水平拉力T的夹角为______.
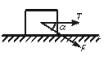
解析:木块受大小为T的水平拉力作用,根据牛顿第二定律有:
T-mgμ=ma
所以μ=
当再施加一推力F时,设此推力与水平拉力T之间的夹角α,由牛顿第二定律有:
在竖直方向 mg+Fsinα=FN
在水平方向 T+Fcosα-FNμ=ma
联立解得 α=arctan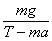
所以本题答案为: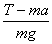 , arctan , arctan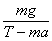
例2.(上海)如图所示,底板光滑的小车上用两个量程为20 N、完全相同的弹簧秤甲和乙系住一个质量为1 kg的物块,在水平地面上,当小车做匀速直线运动时,两弹簧秤的示数均为10 N,当小车做匀加速直线运动时,弹簧秤甲的示数变为8 N,这时小车运动的加速度大小是
A.2 m/s2 B.4 m/s2 C.6 m/s2 D.8 m/s2

解析:
题中两弹簧秤都有示数,说明其弹簧处于伸长的状态.设两弹簧秤示数为10N时,各自伸长量为x,小车做匀加速直线运动时,甲弹簧伸长量为x1.因小车和物块的长度一定,两弹簧原来的总伸长量为2x也保持不变,由此可知,小车做匀加速直线运动时,乙弹簧的伸长量应为(2x-x1),由胡克定律:
匀速时,对甲、乙弹簧有:10=kx
加速时,对甲弹簧有:8=kx1
对乙弹簧有:F乙=k(2x-x1)
联立解得:F乙=12 N
再分析物块有:12-8=ma a=4 m/s2,方向水平向右,故正确答案为B.
例3、如图,质量为m的物体置于摩擦因数为μ的水平面上,现施一与水平面成θ角的拉力F,为使m物体能沿水平面加速运动,试求F的大小范围?
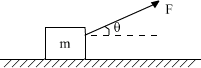
解析:
力F不能太大,否则,物体将离开水平面,有临界条件是地面对物体支持力N≥0。
∴ Fsinθ≤mg,∴ F≤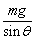
力F不能太小,否则不能沿水平面加速运动,故有物体在水平方向合外力F合>0的临界条件,即:
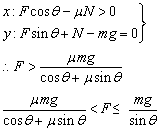
例4、如图,倾角θ=45°的光滑斜面置于光滑的水平面上,质量为m的小球用细线栓在斜面顶端,当斜面以a= g向右运动时,求线的张力T与斜面对球的弹力N。若a= g向右运动时,求线的张力T与斜面对球的弹力N。若a=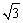 g向右运动,情况又如何? g向右运动,情况又如何?
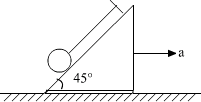
解析:隔离小球,分析小球受力情况如图:以a的方向为坐标轴正方向,有:
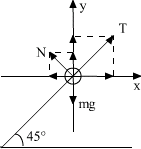
x:Tcos45°-Nsin45°=ma ①
y:Tsin45°+Ncos45°=mg ②
由①②式可得:T=3N代入②,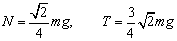
令N=0,a0=gtg45°=g,可见a=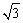 g>a0. g>a0.
小球飞起,设线与竖直面夹角为φ,有: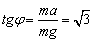 。 。
∴ φ=60° ∴Tcosφ=mg ∴ T=2mg.
注意:a0=g为临界加速度。
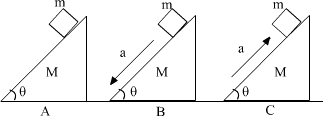
例5、如图,已知滑块质量为m、斜面质量为M,滑块分别在A、B、C三种情况下作匀速下滑、加速下滑、减速下滑、斜面始终不动。讨论地面对斜面体的摩擦力和支持力?
解析:
匀速下滑时,a=0,fA=0,NA=(m+M)g.
加速下滑时,具有向下的加速度ay≠0,失重,NB<(m+M)g。
由整体法可知,f地面=fB=macosθ,方向向左。或用隔离法也可求fB,减速下滑时,ay向上,超重状态,NC>(m+M)g,fC向右。
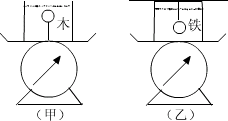
例6、两个完全相同的容器盛满水,置于台秤上,图甲中木球拴于容器底部,乙图中铁球挂于容器上的横杆上,分别剪断细线,则台秤读数各发生什么变化?
解析:
对于甲图,由于木球加速上升,学生很容易误认为超重而使台秤读数变大,其实不然。由于木球上升,对应等体积的“水球”加速下降,整个质心会加速下降,所以台秤读数减小,同理,乙图中台秤读数也减少。
- 返回 -
|